
 mx3-nx+1在[1,+∝)上为增函数的概率是 .
mx3-nx+1在[1,+∝)上为增函数的概率是 .  mx3-nx+1在[1,+∝)上为增函数时,点(m,n)对应的平面区域面积的大小,及m∈[1,6],n∈[1,6]时,点(m,n)对应的平面区域面积的大小,并将它们代入几何概型计算公式进行解答.
mx3-nx+1在[1,+∝)上为增函数时,点(m,n)对应的平面区域面积的大小,及m∈[1,6],n∈[1,6]时,点(m,n)对应的平面区域面积的大小,并将它们代入几何概型计算公式进行解答. mx3-nx+1
mx3-nx+1 mx3-nx+1在[1,+∝)上为增函数
mx3-nx+1在[1,+∝)上为增函数
 mx3-nx+1在[1,+∝)上为增函数的概率P=
mx3-nx+1在[1,+∝)上为增函数的概率P=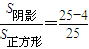 =
=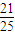
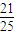
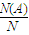 求解.
求解. 

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2009-2010学年辽宁省沈阳市东北育才学校高三(下)5月月考数学试卷(文科)(解析版) 题型:解答题
 mx3-nx+1在[1,+∝)上为增函数的概率是 .
mx3-nx+1在[1,+∝)上为增函数的概率是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com