
ЁОЬтФПЁПФГЙЋЫОдкгаТФъЭэЛсЩЯОйааГщНБЛюЖЏЃЌгаМзЃЌввСНИіГщНБЗНАИЙЉдБЙЄбЁдёЃЎ ЗНАИМзЃКдБЙЄзюЖргаСНДЮГщНБЛњЛсЃЌУПДЮГщНБЕФжаНБТЪОљЮЊ ![]() ЃЌЕквЛДЮГщНБЃЌШєЮДжаНБЃЌдђГщНБНсЪјЃЌШєжаНБЃЌдђЭЈЙ§ХзвЛУЖжЪЕиОљдШЕФгВБвЃЌОіЖЈЪЧЗёМЬајНјааЕкЖўДЮГщНБЃЌЙцЖЈЃКШєХзГігВБвЃЌЗДУцГЏЩЯЃЌдБЙЄдђЛёЕУ500дЊНБН№ЃЌВЛНјааЕкЖўДЮГщНБЃЛШєе§УцГЏЩЯЃЌдБЙЄдђаыНјааЕкЖўДЮГщНБЃЌЧвдкЕкЖўДЮГщНБжаЃЌШєжаНБЃЌдђЛёЕУ1000дЊЃЛШєЮДжаНБЃЌдђЫљЛёЕУНБН№ЮЊ0дЊЃЎ
ЃЌЕквЛДЮГщНБЃЌШєЮДжаНБЃЌдђГщНБНсЪјЃЌШєжаНБЃЌдђЭЈЙ§ХзвЛУЖжЪЕиОљдШЕФгВБвЃЌОіЖЈЪЧЗёМЬајНјааЕкЖўДЮГщНБЃЌЙцЖЈЃКШєХзГігВБвЃЌЗДУцГЏЩЯЃЌдБЙЄдђЛёЕУ500дЊНБН№ЃЌВЛНјааЕкЖўДЮГщНБЃЛШєе§УцГЏЩЯЃЌдБЙЄдђаыНјааЕкЖўДЮГщНБЃЌЧвдкЕкЖўДЮГщНБжаЃЌШєжаНБЃЌдђЛёЕУ1000дЊЃЛШєЮДжаНБЃЌдђЫљЛёЕУНБН№ЮЊ0дЊЃЎ
ЗНАИввЃКдБЙЄСЌајШ§ДЮГщНБЃЌУПДЮжаНБТЪОљЮЊ ![]() ЃЌУПДЮжаНБОљПЩЛёЕУНБН№400дЊЃЎ
ЃЌУПДЮжаНБОљПЩЛёЕУНБН№400дЊЃЎ
ЃЈЂёЃЉЧѓФГдБЙЄбЁдёЗНАИМзНјааГщНБЫљЛёНБН№XЃЈдЊЃЉЕФЗжВМСаЃЛ
ЃЈЂђЃЉЪдБШНЯФГдБЙЄбЁдёЗНАИввгыбЁдёЗНАИМзНјааГщНБЃЌФФИіЗНАИИќЛЎЫуЃП
ЁОД№АИЁПНтЃКЃЈЂёЃЉ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ ЫљвдФГдБЙЄбЁдёЗНАИМзНјааГщНБЫљЛёНБН№XЃЈдЊЃЉЕФЗжВМСаЮЊ
ЃЌ ЫљвдФГдБЙЄбЁдёЗНАИМзНјааГщНБЫљЛёНБН№XЃЈдЊЃЉЕФЗжВМСаЮЊ
X | 0 | 500 | 1000 |
P |
|
|
|
ЃЈЂђЃЉгЩЃЈЂёЃЉПЩжЊЃЌбЁдёЗНАИМзНјааГщНБЫљЛёЕУНБН№XЕФОљжЕ ![]() ЃЌ
ЃЌ
ШєбЁдёЗНАИввНјааГщНБжаНБДЮЪ§ІЮЁЋB ![]() ЃЌдђ
ЃЌдђ ![]() ЃЌ
ЃЌ
ГщНБЫљЛёНБН№XЕФОљжЕEЃЈXЃЉ=EЃЈ400ІЮЃЉ=400EЃЈІЮЃЉ=480ЃЌ
ЙЪбЁдёЗНАИМзНЯЛЎЫу
ЁОНтЮіЁПЃЈIЃЉРћгУЯрЛЅЖРСЂЪТМўЕФИХТЪМЦЫуЙЋЪНМДПЩЕУГіЃЎЃЈIIЃЉРћгУЪ§бЇЦкЭћМЦЫуЙЋЪНЁЂЖўЯюЗжВМСаЕФаджЪМДПЩЕУГіЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
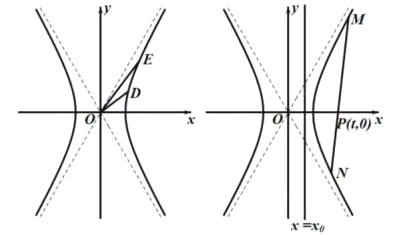
ЁОЬтФПЁПЫЋЧњЯп![]() ЕФащжсГЄЮЊ
ЕФащжсГЄЮЊ![]() ЃЌСНЬѕНЅНќЯпЗНГЬЮЊ
ЃЌСНЬѕНЅНќЯпЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉЧѓЫЋЧњЯп![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЫЋЧњЯп![]() ЩЯгаСНИіЕу
ЩЯгаСНИіЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() КЭ
КЭ![]() ЕФаБТЪжЎЛ§ЮЊ
ЕФаБТЪжЎЛ§ЮЊ![]() ЃЌХаБ№
ЃЌХаБ№![]() ЪЧЗёЮЊЖЈжЕЃЌЃЛ
ЪЧЗёЮЊЖЈжЕЃЌЃЛ
ЃЈ3ЃЉОЙ§Еу![]() ЕФжБЯп
ЕФжБЯп![]() ЧвгыЫЋЧњЯп
ЧвгыЫЋЧњЯп![]() гаСНИіНЛЕу
гаСНИіНЛЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() ЕФЧуаБНЧЪЧ
ЕФЧуаБНЧЪЧ![]() ЃЌЪЧЗёДцдкжБЯп
ЃЌЪЧЗёДцдкжБЯп![]() ЃЈЦфжа
ЃЈЦфжа![]() ЃЉЪЙЕУ
ЃЉЪЙЕУ![]() КуГЩСЂЃПЃЈЦфжа
КуГЩСЂЃПЃЈЦфжа![]() ЗжБ№ЪЧЕу
ЗжБ№ЪЧЕу![]() ЕН
ЕН![]() ЕФОрРыЃЉШєДцдкЃЌЧѓГі
ЕФОрРыЃЉШєДцдкЃЌЧѓГі![]() ЕФжЕЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФжЕЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЬнаЮABCDжаЃЌABЁЮCDЃЌAD=DC=CB=1ЃЌЁЯBCD=120ЁуЃЌЫФБпаЮBFEDЪЧвдBDЮЊжБНЧбќЕФжБНЧЬнаЮЃЌDE=2BF=2ЃЌЦНУцBFEDЁЭЦНУцABCDЃЎ ЃЈЂёЃЉЧѓжЄЃКADЁЭЦНУцBFEDЃЛ
ЃЈЂђЃЉдкЯпЖЮEFЩЯЪЧЗёДцдквЛЕуPЃЌЪЙЕУЦНУцPABгыЦНУцADEЫљГЩЕФШёЖўУцНЧЕФгрЯвжЕЮЊ ![]() ЃЎШєДцдкЃЌЧѓГіЕуPЕФЮЛжУЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЃЎШєДцдкЃЌЧѓГіЕуPЕФЮЛжУЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ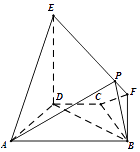
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ= 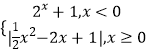 ЃЌЗНГЬf2ЃЈxЃЉЉafЃЈxЃЉ+b=0ЃЈbЁй0ЃЉгаСљИіВЛЭЌЕФЪЕЪ§НтЃЌдђ3a+bЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
ЃЌЗНГЬf2ЃЈxЃЉЉafЃЈxЃЉ+b=0ЃЈbЁй0ЃЉгаСљИіВЛЭЌЕФЪЕЪ§НтЃЌдђ3a+bЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
A.[6ЃЌ11]
B.[3ЃЌ11]
C.ЃЈ6ЃЌ11ЃЉ
D.ЃЈ3ЃЌ11ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕШВюЪ§Са{an}ЕФЧАnЯюКЭЮЊSn ЃЌ ЧвТњзуS4=24ЃЌS7=63ЃЎ ЃЈЂёЃЉЧѓЪ§Са{an}ЕФЭЈЯюЙЋЪНЃЛ
ЃЈЂђЃЉШє ![]() ЃЌЧѓЪ§Са{bn}ЕФЧАnЯюКЭTn ЃЎ
ЃЌЧѓЪ§Са{bn}ЕФЧАnЯюКЭTn ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]()
![]() ЕФзѓНЙЕу
ЕФзѓНЙЕу![]() зѓЖЅЕу
зѓЖЅЕу![]() .
.
ЃЈЂёЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈЂђЃЉвбжЊ![]() ЃЌ
ЃЌ![]() ЪЧЭждВЩЯЕФСНЕуЃЌ
ЪЧЭждВЩЯЕФСНЕуЃЌ![]() ЪЧЭждВЩЯЮЛгкжБЯп
ЪЧЭждВЩЯЮЛгкжБЯп![]() СНВрЕФЖЏЕу.Шє
СНВрЕФЖЏЕу.Шє![]() ЃЌЪдЮЪжБЯп
ЃЌЪдЮЪжБЯп![]() ЕФаБТЪЪЧЗёЮЊЖЈжЕЃПЧыЫЕУїРэгЩ.
ЕФаБТЪЪЧЗёЮЊЖЈжЕЃПЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪЕЪ§aЃЌbЃЌcЃЌdТњзу ![]() =1ЃЌЦфжаeЪЧздШЛЖдЪ§ЕФЕзЪ§ЃЌдђЃЈaЉcЃЉ2+ЃЈbЉdЃЉ2ЕФзюаЁжЕЮЊЃЈ ЃЉ
=1ЃЌЦфжаeЪЧздШЛЖдЪ§ЕФЕзЪ§ЃЌдђЃЈaЉcЃЉ2+ЃЈbЉdЃЉ2ЕФзюаЁжЕЮЊЃЈ ЃЉ
A.4
B.8
C.12
D.18
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
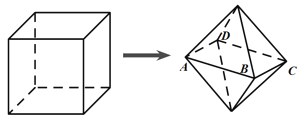
ЁОЬтФПЁПШчЭМЃЌРтГЄЮЊ1ЃЈЕЅЮЛЃК![]() ЃЉЕФе§ЗНЬхФОПщОЙ§ЪЪЕБЧаИюЃЌЕУЕНМИКЮЬх
ЃЉЕФе§ЗНЬхФОПщОЙ§ЪЪЕБЧаИюЃЌЕУЕНМИКЮЬх![]() ЃЌвбжЊМИКЮЬх
ЃЌвбжЊМИКЮЬх![]() гЩСНИіЕзУцЯрЭЌЕФе§ЫФРтзЖзщГЩЃЌЕзУц
гЩСНИіЕзУцЯрЭЌЕФе§ЫФРтзЖзщГЩЃЌЕзУц![]() ЦНаагке§ЗНЬхЕФЯТЕзУцЃЌЧвИїЖЅЕуОљдке§ЗНЬхЕФУцЩЯЃЌдђМИКЮЬх
ЦНаагке§ЗНЬхЕФЯТЕзУцЃЌЧвИїЖЅЕуОљдке§ЗНЬхЕФУцЩЯЃЌдђМИКЮЬх![]() ЬхЛ§ЕФШЁжЕЗЖЮЇЪЧ________ЃЈЕЅЮЛЃК
ЬхЛ§ЕФШЁжЕЗЖЮЇЪЧ________ЃЈЕЅЮЛЃК![]() ЃЉЃЎ
ЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§fЃЈxЃЉ=|x+2|+|xЉa|ЃЌxЁЪR
ЃЈ1ЃЉШєaЃМ0ЃЌЧвlog2fЃЈxЃЉЃО2ЖдШЮвтxЁЪRКуГЩСЂЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєaЃО0ЃЌЧвЙигкxЕФВЛЕШЪНfЃЈxЃЉЃМ ![]() xгаНтЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЎ
xгаНтЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com