
【题目】设函数f(x)=(x﹣a)ex , a∈R. (Ⅰ)当a=1时,试求f(x)的单调增区间;
(Ⅱ)试求f(x)在[1,2]上的最大值;
(Ⅲ)当a=1时,求证:对于x∈[﹣5,+∞), ![]() 恒成立.
恒成立.
【答案】解:(Ⅰ)由f(x)=(x﹣a)ex得f'(x)=(x﹣a+1)ex.
当a=1时,f'(x)=xex,令f'(x)>0,得x>0,
所以f(x)的单调增区间为(0,+∞).
(Ⅱ)令f'(x)=0得x=a﹣1.
所以当a﹣1≤1时,x∈[1,2]时f'(x)≥0恒成立,f(x)单调递增;
当a﹣1≥2时,x∈[1,2]时f'(x)≤0恒成立,f(x)单调递减;
当1<a﹣1<2时,x∈[1,a﹣1)时f'(x)≤0,f(x)单调递减;
x∈(a﹣1,2)时f'(x)>0,f(x)单调递增.
综上,无论a为何值,当x∈[1,2]时,f(x)最大值都为f(1)或f(2).
f(1)=(1﹣a)e,f(2)=(2﹣a)e2,
f(1)﹣f(2)=(1﹣a)e﹣(2﹣a)e2=(e2﹣e)a﹣(2e2﹣e).
所以当 ![]() 时,f(1)﹣f(2)≥0,f(x)max=f(1)=(1﹣a)e.
时,f(1)﹣f(2)≥0,f(x)max=f(1)=(1﹣a)e.
当 ![]() 时,f(1)﹣f(2)<0,
时,f(1)﹣f(2)<0, ![]() .
.
(Ⅲ)令h(x)=f(x)+x,所以h'(x)=xex+1.
所以h'(x)=(x+1)ex.
令h'(x)=(x+1)ex=0,解得x=﹣1,
所以当x∈[﹣5,﹣1),h'(x)<0,h'(x)单调递减;
当x∈[﹣1,+∞),h'(x)>0,h'(x)单调递增.
所以当x=﹣1时, ![]() .
.
所以函数h(x)在[﹣5,+∞)单调递增.
所以 ![]() .
.
所以x∈[﹣5,+∞), ![]() 恒成立
恒成立
【解析】(Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;(Ⅱ)通过讨论a的范围,求出函数的单调区间,求出f(x)的最大值是f(1)或f(2),通过作差求出满足f(1)或f(2)最大时a的范围,从而求出f(x)的最大值;(Ⅲ)令h(x)=f(x)+x,根据函数的单调性求出h(x)的最小值,从而证明结论即可.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )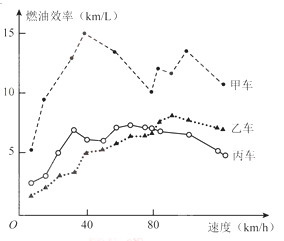
A.消耗1升汽油,乙车最多可行驶5千米
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D.某城市机动车最高限速80千米/小时.相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在(0,+∞)的函数f(x),其导函数为f′(x),满足:f(x)>0且 ![]() 总成立,则下列不等式成立的是( )
总成立,则下列不等式成立的是( )
A.e2e+3f(e)<e2ππ3f(π)
B.e2e+3f(π)>e2ππ3f(e)
C.e2e+3f(π)<e2ππ3f(e)
D.e2e+3f(e)>e2ππ3f(π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知指数函数![]() 满足
满足![]() ,定义域为
,定义域为![]() 的函数
的函数![]() 是奇函数.
是奇函数.
(1)求函数![]() 的解析式;
的解析式;
(2)若函数![]() 在
在![]() 上有零点,求
上有零点,求![]() 的取值范围;
的取值范围;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,E为对角线B1D上的一点,M,N为对角线AC上的两个动点,且线段MN的长度为1. 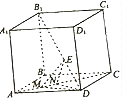
⑴当N为对角线AC的中点且DE= ![]() 时,则三棱锥E﹣DMN的体积是;
时,则三棱锥E﹣DMN的体积是;
⑵当三棱锥E﹣DMN的体积为 ![]() 时,则DE= .
时,则DE= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某市的中学生中随机调查了部分男生,获得了他们的身高数据,整理得到如下频率分布直方图. 
(Ⅰ)求a的值;
(Ⅱ)假设同组中的每个数据用该组区间的中点值代替,估计该市中学生中的全体男生的平均身高;
(Ⅲ)从该市的中学生中随机抽取一名男生,根据直方图中的信息,估计其身高在180cm 以上的概率.若从全市中学的男生(人数众多)中随机抽取3人,用X表示身高在180cm以上的男生人数,求随机变量X的分布列和数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆M: ![]() +y2=1,圆C:x2+y2=6﹣a2在第一象限有公共点P,设圆C在点P处的切线斜率为k1 , 椭圆M在点P处的切线斜率为k2 , 则
+y2=1,圆C:x2+y2=6﹣a2在第一象限有公共点P,设圆C在点P处的切线斜率为k1 , 椭圆M在点P处的切线斜率为k2 , 则 ![]() 的取值范围为( )
的取值范围为( )
A.(1,6)
B.(1,5)
C.(3,6)
D.(3,5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com