【题目】如图1是某条公共汽车线路收支差额
与乘客量的图象.由于目前本条线路亏损，公司有关人员提出了两种扭亏为盈的建议，如图2、3所示.你能根据图象判断下列说法正确的是（ ）
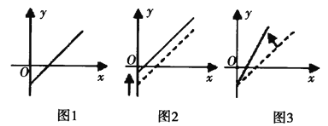
①图2的建议为减少运营成本；②图2的建议可能是提高票价；
③图3的建议为减少运营成本；④图3的建议可能是提高票价.
A.①④B.②④C.①③D.②③
英才计划同步课时高效训练系列答案科目：高中数学 来源： 题型：
【题目】在三棱锥P﹣ABC中，D为AB的中点．
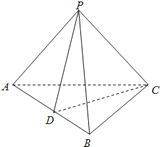
（1）与BC平行的平面PDE交AC于点E，判断点E在AC上的位置并说明理由如下：
（2）若PA=PB，且△PCD为锐角三角形，又平面PCD⊥平面ABC，求证：AB⊥PC．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的左右焦点分别为F1，F2，该椭圆与y轴正半轴交于点M，且△MF1F2是边长为2的等边三角形.
（1）求椭圆的标准方程；
（2）过点F2任作一直线交椭圆于A，B两点，平面上有一动点P，设直线PA，PF2，PB的斜率分别为k1，k，k2，且满足k1+k2=2k，求动点P的轨迹方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，某公园有三条观光大道
、
、
围成直角三角形，其中直角边
，斜边
.
（1）若甲乙都以每分钟100
的速度从点
出发，甲沿
运动，乙沿运动，乙比甲迟2分钟出发，求乙出发后的第1分钟末甲乙之间的距离；
（2）现有甲、乙、丙三位小朋友分别在点
、
、
，设
，乙丙之间的距离
是甲乙之间距离
的2倍，且
，请将甲乙之间的距离
表示为
的函数，并求甲乙之间的最小距离.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司为了获得更大的收益，每年要投入一定的资金用于广告促销，经调查，每年投入广告费t百万元，可增加销售额约为
百万元.
（Ⅰ）若该公司将一年的广告费控制在4百万元之内，则应投入多少广告费，才能使该公司由此增加的收益最大？
（Ⅱ）现该公司准备共投入5百万元，分别用于广告促销和技术改造，经预测，每投入技术改造费
百万元，可增加的销售额约为
百万元，请设计一个资金分配方案，使该公司由此增加的收益最大.
（注：收益=销售额-投入，这里除了广告费和技术改造费，不考虑其他的投入）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设
，
是两条不同的直线，
，
，
是三个不同的平面，给出下列四个命题：（1）若
，
，则
；（2）若
，
，，则
；（3）若
，，则
；（4）若
，
，则,其中正确命题的序号是（ ）
A.（1）（2）B.（2）（3）
C.（3）（4）D.（1）（4）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，已知椭圆
的离心率为
，点
在椭圆上，若圆
的一条切线（斜率存在）与椭圆C有两个交点A，B，且
.
（1）求椭圆的标准方程；
（2）求圆O的标准方程；
（3）已知椭圆C的上顶点为M，点N在圆O上，直线MN与椭圆C相交于另一点Q，且
，求直线MN的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】根据统计，某蔬菜基地西红柿亩产量的增加量
（百千克）与某种液体肥料每亩使用量
（千克）之间的对应数据的散点图，如图所示.
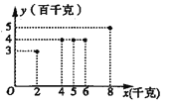
（1）依据数据的散点图可以看出，可用线性回归模型拟合与的关系，请计算相关系数
并加以说明（若
，则线性相关程度很高，可用线性回归模型拟合）；
（2）求关于的回归方程，并预测液体肥料每亩使用量为12千克时，西红柿亩产量的增加量约为多少？
附：相关系数公式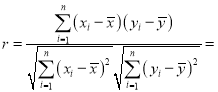
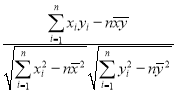，参考数据：
，
.
回归方程
中斜率和截距的最小二乘估计公式分别为：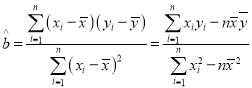
，
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
