
【题目】如图所示,使电路接通,开关不同的开闭方式有( ) 
A.11种
B.20种
C.21种
D.12种
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】下列命题中正确的有 . (填上所有正确命题的序号) ①一质点在直线上以速度v=3t2﹣2t﹣1(m/s)运动,从时刻t=0(s)到t=3(s)时质点运动的路程为15(m);
②若x∈(0,π),则sinx<x;
③若f′(x0)=0,则函数y=f(x)在x=x0取得极值;
④已知函数 ![]() ,则
,则 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() .
.
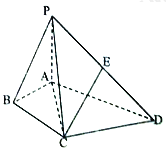
(1)设点![]() 为
为![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角
所成的角![]() 的正弦值为
的正弦值为![]() ?若存在,试确定点
?若存在,试确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O点为坐标原点,且点A(1,0),B(0,1),C(2sinθ,cosθ)
(1)若 ![]() ,求tanθ的值;
,求tanθ的值;
(2)若 ![]() =1,求sinθcosθ的值.
=1,求sinθcosθ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinωx+λcosωx,其图象的一个对称中心到最近的一条对称轴的距离为 ![]() ,且在x=
,且在x= ![]() 处取得最大值.
处取得最大值.
(1)求λ的值.
(2)设 ![]() 在区间
在区间 ![]() 上是增函数,求a的取值范围.
上是增函数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】广东某市一玩具厂生产一种玩具深受大家喜欢,经市场调查该商品每月的销售量![]() (单位:千件)与销售价格
(单位:千件)与销售价格![]() (单位:元/件)满足关系式
(单位:元/件)满足关系式![]() ,其中
,其中![]() ,
, ![]() 为常数.已知销售价格为4元/件时,每日可售出玩具21千件.
为常数.已知销售价格为4元/件时,每日可售出玩具21千件.
(1)求![]() 的值;
的值;
(2)假设该厂生产这种玩具的成本、员工工资等所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格![]() 的值,使该厂每日销售这种玩具所获得的利润最大.(保留1位小数)
的值,使该厂每日销售这种玩具所获得的利润最大.(保留1位小数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com