【答案】
分析:(1)因为对角线互相垂直的四边形ABCD面积

,由于|AC|=d为定长,当|BD|最大时,四边形ABCD面积S取得最大值.由圆的性质,垂直于AC的弦中,直径最长,由此能求出四边形ABCD面积的最大值.
(2)由题意,当点P运动到与圆心M重合时,对角线AC和BD的长同时取得最大值|AC|=|BD|=2r,由此能求出四边形ABCD面积S取得最大值,最大值为2r
2.
(3)类比猜想1:若对角线互相垂直的椭圆内接四边形ABCD中的一条对角线长确定时,当且仅当另一条对角线通过椭圆中心时,该椭圆内接四边形面积最大;类比猜想2:当点P在椭圆中心时,对角线互相垂直的椭圆内接四边形ABCD的面积最大;以上两个均为正确的猜想,要证明以上两个猜想,都需先证:椭圆内的平行弦中,过椭圆中心的弦长最大.类比猜想3:当点P•在椭圆中心,且椭圆内接四边形的两条互相垂直的对角线恰为椭圆长轴和短轴时,四边形面积取得最大值2ab.要证明此猜想,也需先证“椭圆内的平行弦中,过椭圆中心的弦长最大.”
解答:解:(1)因为对角线互相垂直的四边形ABCD面积
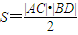
,
而由于|AC|=d为定长,
则当|BD|最大时,四边形ABCD面积S取得最大值.由圆的性质,垂直于AC的弦中,直径最长,
故当且仅当BD过圆心M时,四边形ABCD面积S取得最大值,最大值为dr.
(2)由题意,不难发现,当点P运动到与圆心M重合时,对角线AC和BD的长同时取得最大值|AC|=|BD|=2r,
所以此时四边形ABCD面积S取得最大值,最大值为2r
2.
(3)类比猜想1:若对角线互相垂直的椭圆内接四边形ABCD中的一条对角线长确定时,当且仅当另一条对角线通过椭圆中心时,该椭圆内接四边形面积最大.
类比猜想2:当点P在椭圆中心时,对角线互相垂直的椭圆内接四边形ABCD的面积最大.
以上两个均为正确的猜想,要证明以上两个猜想,都需先证:椭圆内的平行弦中,过椭圆中心的弦长最大.
证:设椭圆的方程为
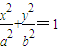
(a>b>0),平行弦MN的方程为y=kx+m,
联立可得b
2x
2+a
2(kx+m)
2-a
2b
2=0⇒(b
2+a
2k
2)x
2+2kma
2x+m
2a
2-a
2b
2=0
不妨设M(x
1,y
1)、N(x
2,y
2),
则
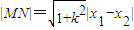
=
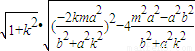
=

=
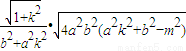
由于平行弦的斜率k保持不变,故可知当且仅当m=0时,即当直线经过原点时,
|MN|取得最大值
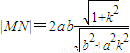
(*).特别地,当斜率不存在时,此结论也成立.
由以上结论可知,类比猜想一正确.又对于椭圆内任意一点P构造的对角线互相垂直的椭圆内接四边形,我们都可以将对角线平移到交点与椭圆中心O重合的椭圆内接四边形A
1B
1C
1D
1,而其中|AC|≤|A
1C
1|,|BD|≤|B
1D
1|,
所以必有
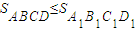
.即证明了猜想二也是正确的.
类比猜想3:当点P•在椭圆中心,且椭圆内接四边形的两条互相垂直的对角线恰为椭圆长轴和短轴时,四边形面积取得最大值2ab.
要证明此猜想,也需先证“椭圆内的平行弦中,过椭圆中心的弦长最大.”在此基础上,可参考以下两种续证方法.
证法一:当点P在椭圆中心时,不妨设对角线AC所在直线的斜率为k.
(i)当k=0时,AC即为椭圆长轴,又AC⊥BD,故BD是椭圆的短轴.
所以此时椭圆内接四边形ABCD的面积为S
ABCD=2ab.
(ii)当k≠0时,对角线BD的斜率为

.由此前证明过程中的(*)可知,
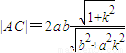
,
若将
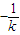
代换式中的k,则可得弦BD的长度,

.
所以,
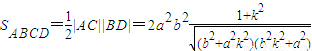
=

=
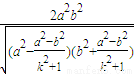
=

=

由k
2+1>1⇒

⇒

,
则
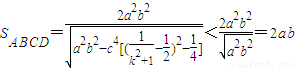
,
综上(i)和(ii),故可证明猜想三正确.
证法二:如图,四边形对角线交点P与椭圆中心重合.
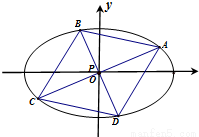
由对称性,不妨设椭圆上的点A的坐标为(acosα,bsinα),
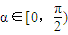
;
相邻的点B坐标为(acosβ,bsinβ),

.由对称性可知,

且当
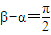
时,S
ABCD取得最大值2ab.
又因为OA⊥OB,故
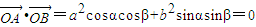
.
由
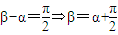
,
所以
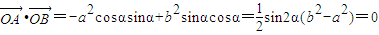
故只有当sin2α=0时才满足,
而因为
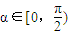
,
故只有当α=0时成立.即由椭圆参数方程的定义,当且仅当点A和点B分别落在椭圆长轴和短轴顶点上时,猜想3正确.
点评:本题考查直线和圆锥曲线的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行类比猜想.

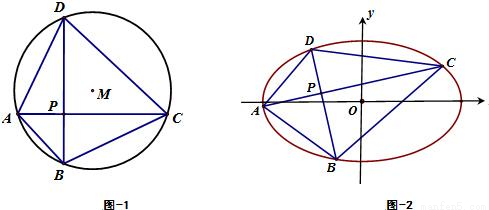
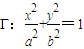 (a>b>0)的内接四边形ABCD的对角线AC和BD相互垂直且交于点P.试提出一个由类比获得的猜想,并尝试给予证明或反例否定.
(a>b>0)的内接四边形ABCD的对角线AC和BD相互垂直且交于点P.试提出一个由类比获得的猜想,并尝试给予证明或反例否定. ,由于|AC|=d为定长,当|BD|最大时,四边形ABCD面积S取得最大值.由圆的性质,垂直于AC的弦中,直径最长,由此能求出四边形ABCD面积的最大值.
,由于|AC|=d为定长,当|BD|最大时,四边形ABCD面积S取得最大值.由圆的性质,垂直于AC的弦中,直径最长,由此能求出四边形ABCD面积的最大值.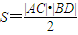 ,
,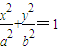 (a>b>0),平行弦MN的方程为y=kx+m,
(a>b>0),平行弦MN的方程为y=kx+m,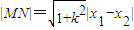
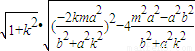

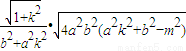
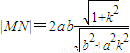 (*).特别地,当斜率不存在时,此结论也成立.
(*).特别地,当斜率不存在时,此结论也成立.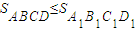 .即证明了猜想二也是正确的.
.即证明了猜想二也是正确的. .由此前证明过程中的(*)可知,
.由此前证明过程中的(*)可知,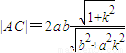 ,
,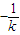 代换式中的k,则可得弦BD的长度,
代换式中的k,则可得弦BD的长度, .
.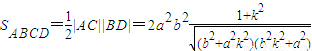

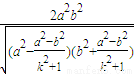


 ⇒
⇒ ,
,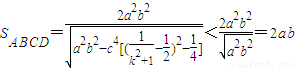 ,
,
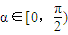 ;
; .由对称性可知,
.由对称性可知,
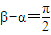 时,SABCD取得最大值2ab.
时,SABCD取得最大值2ab.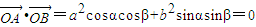 .
.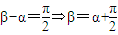 ,
,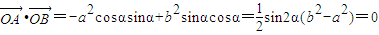
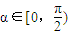 ,
,

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
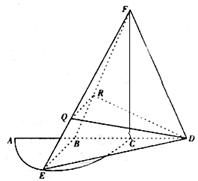
启东小题作业本系列答案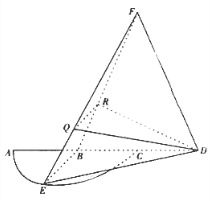 如图,
如图,


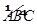 是半径为a的半圆,AC为直径,点E为
是半径为a的半圆,AC为直径,点E为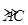 的中点,点B和点C为线段AD的三等分点.平面AEC外一点F满足
的中点,点B和点C为线段AD的三等分点.平面AEC外一点F满足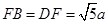 ,FE=
,FE=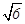 a
.
a
.
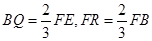 ,求平面
,求平面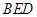 与平面
与平面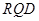 所成二面角的正弦值
所成二面角的正弦值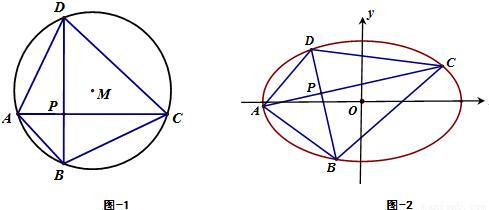
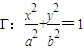 (a>b>0)的内接四边形ABCD的对角线AC和BD相互垂直且交于点P.试提出一个由类比获得的猜想,并尝试给予证明或反例否定.
(a>b>0)的内接四边形ABCD的对角线AC和BD相互垂直且交于点P.试提出一个由类比获得的猜想,并尝试给予证明或反例否定.