
分析 (1)由椭圆基础定义与基本参数意义即可列出方程式;
(2)设h:y=x+m与椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1相切,联立得:9x2+10mx+5m2-10=0;
即h:y=x+3时直线l与h的距离d=$\frac{4}{\sqrt{2}}$,椭圆上动点P到直线L:y=x-1的最大距离,即为△PAB高的最大值;
解答 解:(1)$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{5}}{5}}\\{c=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$⇒$\left\{\begin{array}{l}{{a}^{2}=5}\\{{b}^{2}=4}\end{array}\right.$,则椭圆方程为$\frac{{x}^{2}}{5}+\frac{{y}^{2}}{4}=1$;
(2)设h:y=x+m与椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1相切,联立得:9x2+10mx+5m2-10=0;
∴△=0 得:m2=9,当m=3时,即h:y=x+3时直线l与h的距离d=$\frac{4}{\sqrt{2}}$,
即为椭圆上动点P到直线L:y=x-1的最大距离,亦即为△PAB高的最大值,
∴S△PAB max=$\frac{1}{2}$|AB|dmax=$\frac{1}{2}×\frac{16\sqrt{5}}{9}×\frac{4}{\sqrt{2}}$=$\frac{16\sqrt{10}}{9}$.
点评 本题主要考查了椭圆基本定义与参数,以及直线与椭圆关系综合知识点,属中等题.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:解答题
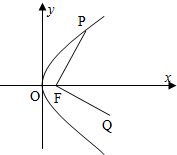 如图,点P是抛物线y2=4x上动点,F为抛物线的焦点,将向量$\overrightarrow{FP}$绕点F按顺时针方向旋转90°到$\overrightarrow{FQ}$
如图,点P是抛物线y2=4x上动点,F为抛物线的焦点,将向量$\overrightarrow{FP}$绕点F按顺时针方向旋转90°到$\overrightarrow{FQ}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
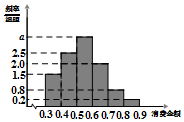 某电商对10000名网购者2015年度消费情况进行统计,其消费频率分布直方图如图,则在这些网购者中,消费金额在[0.5,0.9]内的人数为( )
某电商对10000名网购者2015年度消费情况进行统计,其消费频率分布直方图如图,则在这些网购者中,消费金额在[0.5,0.9]内的人数为( )| A. | 2000 | B. | 4500 | C. | 6000 | D. | 7500 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
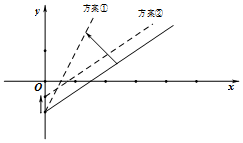 如图是某条公共汽车线路收支差额y与乘客量x的图象(实线),由于目前本线路亏损,公司有关人员提出两种扭亏为盈的方案(虚线),这两种方案分别是( )
如图是某条公共汽车线路收支差额y与乘客量x的图象(实线),由于目前本线路亏损,公司有关人员提出两种扭亏为盈的方案(虚线),这两种方案分别是( )| A. | 方案①降低成本,票价不变,方案②提高票价而成本不变; | |
| B. | 方案①提高票价而成本不变,方案②降低成本,票价不变; | |
| C. | 方案①降低成本,票价提高,方案②提高票价而成本不变; | |
| D. | 方案①提高成本,票价不变,方案②降低票价且成本降低 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com