
【题目】正方体![]() 的棱长为
的棱长为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() ,
,![]() 的中点,则过
的中点,则过![]() 且与
且与![]() 平行的平面截正方体所得截面的面积为______,
平行的平面截正方体所得截面的面积为______,![]() 和该截面所成角的正弦值为______.
和该截面所成角的正弦值为______.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为了研究“教学方式”对教学质量的影响,某高中老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.

甲班 | 乙班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
![]() 现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学至少有一名被抽中的概率;
现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学至少有一名被抽中的概率;
(II)学校规定:成绩不低于75分的为优秀.请填写下面的2×2列联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
下面临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | .024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2=![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,
中,![]() 均垂直于平面
均垂直于平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
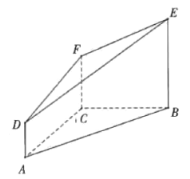
(1)过![]() 的平面
的平面![]() 与平面
与平面![]() 垂直,请在图中作出
垂直,请在图中作出![]() 截此多面体所得的截面,并说明理由;
截此多面体所得的截面,并说明理由;
(2)若![]() ,
,![]() ,求多面体
,求多面体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() (
(![]() )的左、右焦点为
)的左、右焦点为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() .已知
.已知![]() .
.
(1)求椭圆的离心率;
(2)设![]() 为椭圆上异于其顶点的一点,以线段
为椭圆上异于其顶点的一点,以线段![]() 为直径的圆经过点
为直径的圆经过点![]() ,经过原点
,经过原点![]() 的直线
的直线![]() 与该圆相切,求直线
与该圆相切,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点M到定点F1(-2,0)和F2(2,0)的距离之和为![]() .
.
(1)求动点M轨迹C的方程;
(2)设N(0,2),过点P(-1,-2)作直线l,交椭圆C于不同于N的A,B两点,直线NA,NB的斜率分别为k1,k2,问k1+k2是否为定值?若是的求出这个值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网络外卖也开始成为不少人日常生活中不可或缺的一部分![]() 市某调查机构针对该市市场占有率最高的两种网络外卖企业
市某调查机构针对该市市场占有率最高的两种网络外卖企业![]() 以下简称外卖A、外卖
以下简称外卖A、外卖![]() 的服务质量进行了调查,从使用过这两种外卖服务的市民中随机抽取了1000人,每人分别对这两家外卖企业评分,满分均为100分,并将分数分成5组,得到以下频数分布表:
的服务质量进行了调查,从使用过这两种外卖服务的市民中随机抽取了1000人,每人分别对这两家外卖企业评分,满分均为100分,并将分数分成5组,得到以下频数分布表:
分数 人数 种类 |
|
|
|
|
|
外卖A | 50 | 150 | 100 | 400 | 300 |
外卖B | 100 | 100 | 300 | 200 | 300 |
表中得分越高,说明市民对网络外卖服务越满意![]() 若得分不低于60分,则表明该市民对网络外卖服务质量评价较高
若得分不低于60分,则表明该市民对网络外卖服务质量评价较高![]() 现将分数按“服务质量指标”划分成以下四个档次:
现将分数按“服务质量指标”划分成以下四个档次:
分数 |
|
|
|
|
服务质量指标 | 0 | 1 | 2 | 3 |
视频率为概率,解决下列问题:
![]() 从该市使用过外卖A的市民中任选5人,记对外卖A服务质量评价较高的人数为X,求X的数学期望.
从该市使用过外卖A的市民中任选5人,记对外卖A服务质量评价较高的人数为X,求X的数学期望.
![]() 从参与调查的市民中随机抽取1人,试求其评分中外卖A的“服务质量指标”与外卖B的“服务质量指标”的差的绝对值等于2的概率;
从参与调查的市民中随机抽取1人,试求其评分中外卖A的“服务质量指标”与外卖B的“服务质量指标”的差的绝对值等于2的概率;
![]() 在M市工作的小王决定从外卖A、外卖B这两种网络外卖中选择一种长期使用,如果从这两种外卖的“服务质量指标”的期望角度看,他选择哪种外卖更合适?试说明理由.
在M市工作的小王决定从外卖A、外卖B这两种网络外卖中选择一种长期使用,如果从这两种外卖的“服务质量指标”的期望角度看,他选择哪种外卖更合适?试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,平面DAC⊥底面ABC,![]() ,AD=CD=
,AD=CD=![]() ,O是AC的中点,E是BD的中点.
,O是AC的中点,E是BD的中点.
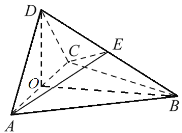
(1)证明:DO⊥底面ABC;
(2)求二面角D-AE-C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com