练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
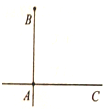
    如图，两高速公路线垂直相交于站A，若已知AB=100千米，甲汽车从A站出发，沿AC方向以50千米/小时的速度行驶，同时乙汽车从B站出发，一年BA方向以v千米/小时的速度行驶，至A站即停止前行（甲车仍继续行驶）（两车的车长忽略不计）．
    （1）甲、乙两车的最近距离为
     
    （用含v的式子表示）；
    （2）若甲、乙两车从开始行驶到甲、乙两车相距最近时所用时间为t0小时，则当v为
     
    时t0最大．
    考点：函数模型的选择与应用
    专题：函数的性质及应用
    分析：（1）设乙车行驶t小时到D，甲车行驶t小时到E，分类讨论，利用二次函数确定最值；
    （2）利用基本不等式，即可求得结论．
    解答： 解：（1）设乙车行驶t小时到D，甲车行驶t小时到E
    若0≤vt≤100，则DE2=AE2+AD2=（100-vt）2+（50t）2=（2500+v2）t2-200vt+10000
    ∴t=
    100v
    		2500+v2
    时，DE2取到最小值，DE也取到最小值，最小值为
    5000
    		2500+v2
    ；
    若vt＞100，乙车停止，甲车继续前行，DE越来越大，无最大值
    综上，甲，乙两车的最近距离为
    5000
    		2500+v2
    千米；
    （2）t0=
    100v
    2500+v2
    =
    100
    2500
    v
    +v
    ≤
    100
    100
    =1，
    当且仅当v=
    2500
    v
    ，即v=50千米/小时，t0最大，
    故答案为：
    5000
    		2500+v2
    ；50千米/小时；
    点评：本题考查函数模型的构建，考查基本不等式的运用，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知A（-3，1），B（3，1），C（1，3），则△ABC中BC边上的高所在的直线方程为（　　）
    A、x+y=0
    B、x-y+4=0
    C、x+y+2=0
    D、x-y=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

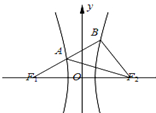    如图，F1，F2是双曲线C：
    x2
    a2
    -
    y2
    b2
    =1    （a＞0，b＞0）的左、右焦点，过F1的直线l与C的左、右两支分别交于A，B两点．若△ABF2为等边三角形，则双曲线的离心率为（　　）
    A、
    		6
    2
    B、
    		3
    C、
    		5
    +1
    2
    D、
    		7

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    我们定义函数y=[x]（[x]表示不大于x的最大整数）为“下整函数”；定义y={x}（{x}表示不小于x的最小整数）为“上整函数”；例如[4.3]=4，[5]=5；{4.3}=5，{5}=5．某停车场收费标准为每小时2元，即不超过1小时（包括1小时）收费2元，超过一小时，不超过2小时（包括2小时）收费4元，以此类推．若李刚停车时间为x小时，则李刚应缴费为（单位：元）（　　）
    A、2[x+1]
    B、2（[x]+1）
    C、2{x}
    D、{2x}

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知数列{an}，其前n项和为Sn，若a2=4，2Sn=an（n+1），求a1，a3及数列{an}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

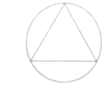    某人随机地向如图所示的正三角形及其外接圆区域内部设计（不包括三角形及其外接圆的边界），则针孔到正三角形内部（不包括边界）的概率为（　　）
    A、
    3
    		3
    2π
    B、
    		3
    π
    C、
    3
    		3
    4π
    D、
    3
    		3
    5π

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若从区间（0，e）内随机取两个数，则这两个数之积不小于e的概率为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    空间四边形ABCD中，若E、F、G、H分别为AB、BC、CD、DA边上的中点，则下列各式中成立的是（　　）
    A、
    EB
    +
    BF
    +
    EH
    +
    GH
    =0
    B、
    EB
    +
    FC
    +
    EH
    -
    EG
    =0
    C、
    EF
    +
    FG
    +
    EH
    +
    GH
    =0
    D、
    EF
    -
    FB
    +
    CG
    +
    GH
    =0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    球O是四面体ABCD的外接球（即四面体的顶点均在球面上），若DB⊥平面ABC，AB⊥AC，且AC=1，DB=AB=2，则球O的表面积为（　　）
    A、10πB、9πC、8πD、7π

    查看答案和解析>>

    同步练习册答案