
| A. | $y=±\frac{\sqrt{2}}{2}x$ | B. | $y=±\sqrt{2}x$ | C. | y=±2x | D. | y=$±\frac{1}{2}x$ |
分析 利用$\frac{1}{k}$和e是方程${x}^{2}+mx+\sqrt{6}=0$的两个根,可得$\frac{e}{k}$=$\sqrt{6}$,结合离心率公式,可得$\frac{\sqrt{1+\frac{1}{{k}^{2}}}}{k}$=$\sqrt{6}$,求出k,即可求出双曲线的渐近线方程.
解答 解:∵$\frac{1}{k}$和e是方程${x}^{2}+mx+\sqrt{6}=0$的两个根,
∴$\frac{e}{k}$=$\sqrt{6}$,
∴$\frac{\sqrt{1+\frac{1}{{k}^{2}}}}{k}$=$\sqrt{6}$,
∴k=$\frac{\sqrt{2}}{2}$,
∴该双曲线的渐近线方程为y=±$\frac{\sqrt{2}}{2}$x,
故选:A.
点评 本题考查双曲线的渐近线方程,考查学生的计算能力,属于中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:解答题
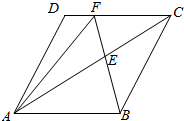 如图,在菱形ABCD中,AB=1,∠BAD=60°,且E为对角线AC上一点.
如图,在菱形ABCD中,AB=1,∠BAD=60°,且E为对角线AC上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$,$\frac{1}{6}$R3 | B. | $\frac{π}{3}$,$\frac{1}{3}$R3 | C. | $\frac{π}{2}$,$\frac{1}{3}$R3 | D. | $\frac{π}{2}$,$\frac{1}{6}$R3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
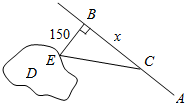 如图,一海岛D,海岛离岸边最近点B的距离是150km,在岸边距点B300km的点A处有一批物资需运往海岛D,为了尽快送达海岛,A与B之间有一铁路,现用海陆联运的方式,火车的时速为50km,船的时速为30km,试在岸边选一点C,问选在何处可使运输时间最短.
如图,一海岛D,海岛离岸边最近点B的距离是150km,在岸边距点B300km的点A处有一批物资需运往海岛D,为了尽快送达海岛,A与B之间有一铁路,现用海陆联运的方式,火车的时速为50km,船的时速为30km,试在岸边选一点C,问选在何处可使运输时间最短.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com