
【题目】直角坐标系中曲线![]() 的参数方程:
的参数方程:![]() (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,
轴正半轴为极轴的极坐标系中,![]() 点的极坐标
点的极坐标![]() ,在平面直角坐标系中,直线
,在平面直角坐标系中,直线![]() 经过点
经过点![]() ,倾斜角为
,倾斜角为![]() .
.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】有三种股票,前两种的股数之和等于第三种的股数, 第二种股票的总价值是第一种股票的4 倍,第一、二种股票的总价值等于第三种股票的总价值,第二种股票每股比第一种股票贵![]() 元到2元,而第三种股票每股的价值不小于
元到2元,而第三种股票每股的价值不小于![]() 元而不大于6元.求在股票总量中第一种股票股数占总股数的百分比的最大值与最小值.
元而不大于6元.求在股票总量中第一种股票股数占总股数的百分比的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周上有800个点,依顺时针方向标号为![]() ,它们将圆周分成800个间隙.今选定某一点染成红色,然后按如下规则,逐次染红其余的一些点:如果第
,它们将圆周分成800个间隙.今选定某一点染成红色,然后按如下规则,逐次染红其余的一些点:如果第![]() 号点已被染红,则可按顺时针方向转过
号点已被染红,则可按顺时针方向转过![]() 个间隙,再将所到达的那个端点染红.如此继续下去.试问圆周上最多可得到多少个红点?证明你的结论.
个间隙,再将所到达的那个端点染红.如此继续下去.试问圆周上最多可得到多少个红点?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
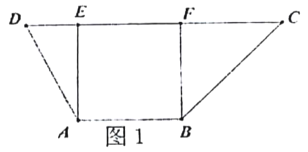
【题目】在梯形![]() 中(图1),
中(图1),![]() ,
, ![]() ,
, ![]() ,过
,过![]() 、
、![]() 分别作
分别作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() 、
、![]() ,已知
,已知![]() ,
, ![]() ,将梯形
,将梯形![]() 沿
沿![]() 、
、![]() 同侧折起,使得
同侧折起,使得![]() ,
, ![]() ,得空间几何体
,得空间几何体![]() (图2).
(图2).
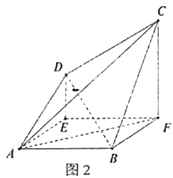
(1)证明: ![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春,新型冠状病毒在我国湖北武汉爆发并讯速蔓延,病毒传染性强并严重危害人民生命安全,国家卫健委果断要求全体人民自我居家隔离,为支援湖北武汉新型冠状病毒疫情防控工作,各地医护人员纷纷逆行,才使得病毒蔓延得到了有效控制.某社区为保障居民的生活不受影响,由社区志愿者为其配送蔬菜、大米等生活用品,记者随机抽查了男、女居民各100名对志愿者所买生活用品满意度的评价,得到下面的2×2列联表.
特别满意 | 基本满意 | |
男 | 80 | 20 |
女 | 95 | 5 |
(1)被调查的男性居民中有5个年轻人,其中有2名对志愿者所买生活用品特别满意,现在这5名年轻人中随机抽取3人,求至多有1人特别满意的概率.
(2)能否有99%的把握认为男、女居民对志愿者所买生活用品的评价有差异?
附: 
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,侧面
为平行四边形,侧面![]() 底面
底面![]() .已知
.已知![]() ,
,![]() ,
,![]() ,
,![]() .
.
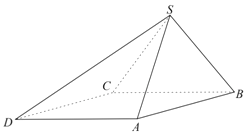
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() ?若存在,请求出
?若存在,请求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com