
设函数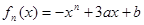 (
(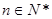 ,
,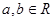 )。
)。
⑴若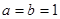 ,求
,求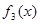 在
在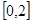 上的最大值和最小值;
上的最大值和最小值;
⑵若对任意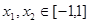 ,都有
,都有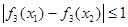 ,求
,求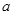 的取值范围;
的取值范围;
⑶若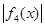 在
在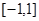 上的最大值为
上的最大值为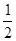 ,求
,求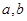 的值。
的值。
(1)最大值为3,最小值为-1;(2)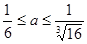 ;(3)
;(3)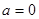 ,
,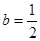 .
.
【解析】
试题分析:(1)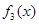 是三次函数,要求它的最大值和最小值一般利用导数来求,具体的就是令
是三次函数,要求它的最大值和最小值一般利用导数来求,具体的就是令 ,求出
,求出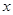 ,再讨论相应区间的单调性,就可判断出函数什么时候取最大值,什么时候取最小值;(2)要求
,再讨论相应区间的单调性,就可判断出函数什么时候取最大值,什么时候取最小值;(2)要求 的取值范围,题中没有其他的信息,因此我们首先判断出
的取值范围,题中没有其他的信息,因此我们首先判断出 的初始范围,由已知有
的初始范围,由已知有 ,得出
,得出 ,而此时
,而此时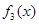 在
在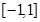 上的单调性不确定,通过讨论单调性,求出
上的单调性不确定,通过讨论单调性,求出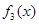 在
在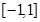 上的最大值和最小值,为什么要求最大值
上的最大值和最小值,为什么要求最大值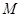 和最小值
和最小值 呢?原因就在于题设条件等价于最大值与最小值的差
呢?原因就在于题设条件等价于最大值与最小值的差 ,这样就有求出
,这样就有求出 的取值范围了;(3)对
的取值范围了;(3)对 在
在 上的最大值为
上的最大值为 的处理方法,同样我们用特殊值法,首先
的处理方法,同样我们用特殊值法,首先 ,即
,即 ,由这两式可得
,由这两式可得 ,而特殊值
,而特殊值 ,又能得到
,又能得到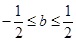 ,那么只能有
,那么只能有 ,把
,把 代入
代入 和
和 ,就可求出
,就可求出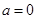 .
.
试题解析:(1) ,∴
,∴ , 2分
, 2分
∴在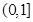 内,
内, ,在
,在 内,
内, ,
,
∴在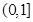 内,
内, 为增函数,在
为增函数,在 内,
内, 为减函数,
为减函数,
∴ 的最大值为
的最大值为 ,最小值为
,最小值为 , 4分
, 4分
(2)∵对任意 有
有 ,∴
,∴ ,
,
从而有 ,∴
,∴ . 6分
. 6分
又 ,∴
,∴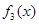 在
在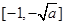 ,
, 内为减函数,在
内为减函数,在 内为增函数,只需
内为增函数,只需 ,则
,则 ,
,
∴ 的取值范围是
的取值范围是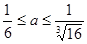 10分[
10分[
(3)由 知
知 ①
① ②,
②,
①加②得 又∵
又∵ ∴
∴ ∴
∴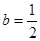 14分
14分
将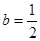 代入①②得
代入①②得 ∴
∴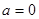 16分
16分
考点:(1)函数的最值;(2)导数的应用;(3)含绝对值的函数的最大值与不等式的综合知识.


科目:高中数学 来源: 题型:
| mx |
| x2+n |
| a |
| x |
| 7 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 4x |
| 4x+2 |
| 1 |
| 1001 |
| 2 |
| 1001 |
| 3 |
| 1001 |
| 1000 |
| 1001 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com