
【题目】如图,在以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的五面体中,面
为顶点的五面体中,面![]() 为正方形,
为正方形,![]() ,
,![]() ,且二面角
,且二面角![]() 与二面角
与二面角![]() 都是
都是![]() .
.
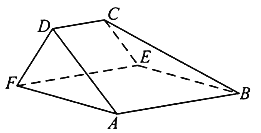
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①如果![]() ,
,![]() 是两条直线,且
是两条直线,且![]() ,那么
,那么![]() 平行于经过
平行于经过![]() 的任何平面;
的任何平面;
②如果直线![]() 和平面
和平面![]() 满足
满足![]() ,那么直线
,那么直线![]() 与平面
与平面![]() 内的任何直线平行;
内的任何直线平行;
③如果直线![]() ,
,![]() 和平面
和平面![]() 满足
满足![]() ,
,![]() ,那么
,那么![]() ;
;
④如果直线![]() ,
,![]() 和平面
和平面![]() 满足
满足![]() ,
,![]() ,
,![]() ,那么
,那么![]() ;
;
⑤如果平面![]() ,
,![]() ,
,![]() 满足
满足![]() ,
,![]() ,那么
,那么![]() .
.
其中正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() ABC中,角A,B,C的对边分别是a,b,c,已知2acosA=-
ABC中,角A,B,C的对边分别是a,b,c,已知2acosA=-![]() (ccosB+bcosC)。
(ccosB+bcosC)。
(1)求角A;
(2)若b=2,且![]() ABC的面积为
ABC的面积为![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数  ,若m<n,且f(m)=f(n),则n﹣m的取值范围是( )
,若m<n,且f(m)=f(n),则n﹣m的取值范围是( )
A.[3﹣2ln2,2)
B.[3﹣2ln2,2]
C.[e﹣1,2]
D.[e﹣1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本为
千件,需另投入成本为![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元).当年产量不小于80千件时
(万元).当年产量不小于80千件时![]() (万元).每件商品售价为0.05万元.通过分析,该工厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过分析,该工厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在实数集R上定义一种运算“*”,对于任意给定的a、b∈R,a*b为唯一确定的实数,且具有性质:
1)对任意a、b∈R,a*b=b*a;
2)对任意a、b∈R,a*0=a;
3)对任意a、b∈R,(a*b)*c=c*(ab)+(a*c)+(c*b)﹣2c.
关于函数f(x)=x* ![]() 的性质,有如下说法:
的性质,有如下说法:
①在(0,+∞)上函数f(x)的最小值为3;
②函数f(x)为奇函数;
③函数f(x)的单调递增区间为(﹣∞,﹣1),(1,+∞).
其中所有正确说法的个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com