
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处切线与直线
处切线与直线![]() 垂直(其中
垂直(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)求![]() 的解析式及单调减区间;
的解析式及单调减区间;
(2)是否存在常数![]() ,使得对于定义域的任意
,使得对于定义域的任意![]() 恒成立,若存在,求出
恒成立,若存在,求出 ![]() 的值;若
的值;若
不存在,说明理由.
 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】刘徽是我国魏晋时期著名的数学家,他编著的《海岛算经》中有一问题:“今有望海岛,立两表齐,高三丈,前后相去千步,令后表与前表相直。从前表却行一百二十三步,人目著地取望岛峰,与表末参合。从后表却行百二十七步,人目著地取望岛峰,亦与表末参合。问岛高几何?” 意思是:为了测量海岛高度,立了两根表,高均为5步,前后相距1000步,令后表与前表在同一直线上,从前表退行123步,人恰观测到岛峰,从后表退行127步,也恰观测到岛峰,则岛峰的高度为( )(注:3丈=5步,1里=300步)
A. 4里55步 B. 3里125步 C. 7里125步 D. 6里55步
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 相邻两对称轴间的距离为
相邻两对称轴间的距离为![]() ,若将
,若将![]() 的图像先向左平移
的图像先向左平移![]() 个单位,再向下平移1个单位,所得的函数
个单位,再向下平移1个单位,所得的函数![]() 为奇函数.
为奇函数.
(1)求![]() 的解析式,并求
的解析式,并求![]() 的对称中心;
的对称中心;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不相等的实根,求实数
上有两个不相等的实根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某种微生物的生长规律,需要了解环境温度![]() (
(![]() )对该微生物的活性指标
)对该微生物的活性指标![]() 的影响,某实验小组设计了一组实验,并得到如表的实验数据:
的影响,某实验小组设计了一组实验,并得到如表的实验数据:
环境温度 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
活性指标 |
|
|
|
|
|
|
|
(Ⅰ)由表中数据判断![]() 关于
关于![]() 的关系较符合
的关系较符合![]() 还是
还是![]() ,并求
,并求![]() 关于
关于![]() 的回归方程(
的回归方程(![]() ,
,![]() 取整数);
取整数);
(Ⅱ)根据(Ⅰ)中的结果分析:若要求该种微生物的活性指标不能低于![]() ,则环境温度应不得高于多少
,则环境温度应不得高于多少![]() ?
?
附: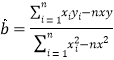 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了对某课题进行研究,用分层抽样方法从三所高校![]() 的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
高校 | 相关人数 | 抽取人数 |
A | 18 |
|
B | 36 | 2 |
C | 54 |
|
(Ⅰ)求![]() ,
,![]() ;
;
(Ⅱ)若从高校![]() 抽取的人中选2人作专题发言,求这二人都来自高校
抽取的人中选2人作专题发言,求这二人都来自高校![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,
, ![]() 是焦点,直线
是焦点,直线![]() 是经过点
是经过点![]() 的任意直线.
的任意直线.
(Ⅰ)若直线![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点,且
两点,且![]() (
(![]() 是坐标原点,
是坐标原点, ![]() 是垂足),求动点
是垂足),求动点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)若![]() 、
、![]() 两点在抛物线
两点在抛物线![]() 上,且满足
上,且满足![]() ,求证:直线
,求证:直线![]() 必过定点,并求出定点的坐标.
必过定点,并求出定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com