
(13分)(2011•重庆)某市公租房的房源位于A、B、C三个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,求该市的任4位申请人中:
(Ⅰ)恰有2人申请A片区房源的概率;
(Ⅱ)申请的房源所在片区的个数的ξ分布列与期望.
(Ⅰ)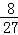 (Ⅱ)ξ的分布列是:
(Ⅱ)ξ的分布列是:
∴Eξ=ξ 1 2 3 P 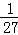
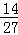
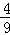
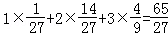
解析试题分析:(I)本题是一个等可能事件的概率,试验发生包含的事件是4个人中,每一个人有3种选择,共有34种结果,满足条件的事件是恰有2人申请A片区房源,共有C4222,得到概率.
(II)由题意知变量ξ的可能取值是1,2,3,结合变量对应的事件和第一问的做法写出变量对应的概率,写出分布列,做出变量的期望值.
解:(I)由题意知本题是一个等可能事件的概率
试验发生包含的事件是4个人中,每一个人有3种选择,共有34种结果,
满足条件的事件是恰有2人申请A片区房源,共有C4222
∴根据等可能事件的概率公式得到P=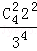 =
=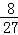
(II)由题意知ξ的可能取值是1,2,3
P(ξ=1)=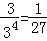 ,
,
P(ξ=2)=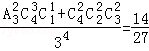 ,
,
P(ξ=3)=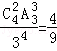
∴ξ的分布列是:
∴Eξ=ξ 1 2 3 P 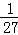
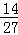
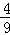
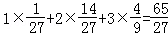
点评:本题考查等可能事件的概率,考查离散型随机变量的分布列和期望,求离散型随机变量的分布列和期望是近年来理科高考必出的一个问题,题目做起来不难,运算量也不大,只要注意解题格式就问题不大.


科目:高中数学 来源: 题型:解答题
我国政府对PM2.5采用如下标准:
| PM2.5日均值m(微克/立方米) | 空气质量等级 |
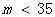 | 一级 |
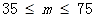 | 二级 |
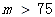 | 超标 |

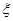 表示空气质量达到一级的天数,求
表示空气质量达到一级的天数,求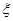 的分布列;
的分布列;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
将连续正整数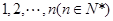 从小到大排列构成一个数
从小到大排列构成一个数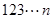 ,
,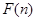 为这个数的位数(如
为这个数的位数(如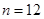 时,此数为
时,此数为 ,共有15个数字,
,共有15个数字, ),现从这个数中随机取一个数字,
),现从这个数中随机取一个数字,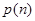 为恰好取到0的概率.
为恰好取到0的概率.
(1)求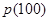 ;
;
(2)当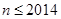 时,求
时,求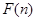 的表达式;
的表达式;
(3)令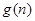 为这个数中数字0的个数,
为这个数中数字0的个数,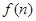 为这个数中数字9的个数,
为这个数中数字9的个数,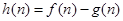 ,
, ,求当
,求当 时
时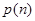 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某超市在节日期间进行有奖促销,规定凡在该超市购物满400元的顾客,均可获得一次摸奖机会.摸奖规则如下:
奖盒中放有除颜色不同外其余完全相同的4个球(红、黄、黑、白).顾客不放回的每次摸出1个球,若摸到黑球则摸奖停止,否则就继续摸球.按规定摸到红球奖励20元,摸到白球或黄球奖励10元,摸到黑球不奖励.
(1)求1名顾客摸球2次摸奖停止的概率;
(2)记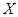 为1名顾客摸奖获得的奖金数额,求随机变量
为1名顾客摸奖获得的奖金数额,求随机变量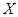 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为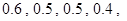 各人是否需使用设备相互独立.
各人是否需使用设备相互独立.
(1)求同一工作日至少3人需使用设备的概率;
(2)X表示同一工作日需使用设备的人数,求X的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
地为绿化环境,移栽了银杏树 棵,梧桐树
棵,梧桐树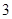 棵.它们移栽后的成活率分别
棵.它们移栽后的成活率分别
为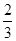 、
、 ,每棵树是否存活互不影响,在移栽的
,每棵树是否存活互不影响,在移栽的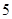 棵树中:
棵树中:
(1)求银杏树都成活且梧桐树成活 棵的概率;
棵的概率;
(2)求成活的棵树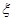 的分布列与期望.
的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
| API | 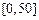 | 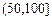 | 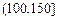 | 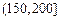 | 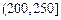 | 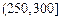 | 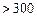 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
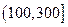 对企业造成经济损失成直线模型(当API为150时造成的 经济损失为500元,当API为200时,造成的经济损失为700元);当API大于300时造成的 经济损失为2000元;
对企业造成经济损失成直线模型(当API为150时造成的 经济损失为500元,当API为200时,造成的经济损失为700元);当API大于300时造成的 经济损失为2000元;
|
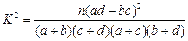
| | 非重度污染 | 重度污染 | 合计 |
| 供暖季 | | | |
| 非供暖季 | | | |
| 合计 | | | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
现有10名教师,其中男教师6名,女教师4名.
(1)要从中选2名教师去参加会议,有多少种不同的选法?
(2)现要从中选出4名教师去参加会议,求男、女教师各选2名的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
根据以往的经验,某工程施工期间的降水量X(单位:mm)对工期的影响如下表:
| 降水量X | 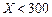 | 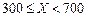 | 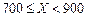 | 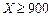 |
工期延误天数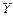 | 0 | 2 | 6 | 10 |
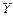 的均值与方差;(2)在降水量X至少是300的条件下,工期延误不超过6天的概率.
的均值与方差;(2)在降水量X至少是300的条件下,工期延误不超过6天的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com