
如图,已知C点在圆O直径BE的延长线上,CA切圆O于A点,DC是∠ACB的平分线交AE于点F,交AB于D点.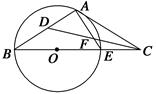
(1)求∠ADF的度数;
(2)AB=AC,求AC∶BC.
(1) ∠ADF=45°; (2) AC∶BC= .
.
解析试题分析:(1)由弦切角与角平分线,三角形的外角可得∠ADF=∠AFD,BE为直径∠DAE=90°,则可得∠ADF=45°;(2)由△ACE∽△BCA得 ,在
,在 中可得比值.
中可得比值.
解(1)∵AC为圆O的切线,∴∠B=∠EAC,
又知DC是∠ACB的平分线,∴∠ACD=∠DCB,
∴∠B+∠DCB=∠EAC+∠ACD,
即∠ADF=∠AFD,又因为BE为圆O的直径,
∴∠DAE=90°,∴∠ADF= (180°-∠DAE)=45°. 5分
(180°-∠DAE)=45°. 5分
(2)∵∠B=∠EAC,∠ACB=∠ACB,
∴△ACE∽△BCA,
∴ ,又∵AB=AC,∠ADF=45°,
,又∵AB=AC,∠ADF=45°,
∴∠B=∠ACB=30°,
∴在 中,
中, =tan∠B=tan 30°=
=tan∠B=tan 30°= . 10分
. 10分
考点:弦切角,三角形的相似的性质与判定.


科目:高中数学 来源: 题型:解答题
如图,EP交圆于E、C两点,PD切圆于D,G为CE上一点且 ,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
(1)求证:AB为圆的直径;
(2)若AC=BD,求证: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,EP交圆于E、C两点,PD切圆于D,G为CE上一点且 ,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
(1)求证:AB为圆的直径;
(2)若AC=BD,求证:AB=ED.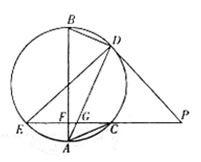
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图, ,
, 分别为
分别为 的边
的边 ,
, 上的点,且不与
上的点,且不与 的顶点重合。已知
的顶点重合。已知 的长为
的长为 ,AC的长为n,
,AC的长为n, ,
, 的长是关于
的长是关于 的方程
的方程 的两个根。
的两个根。
(1)证明: ,
, ,
, ,
, 四点共圆;
四点共圆;
(2)若 ,且
,且 ,求
,求 ,
, ,
, ,
, 所在圆的半径。
所在圆的半径。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com