
【题目】如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则它的体积为 . 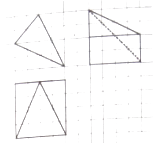
 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
【题目】对实数a和b,定义运算“”:ab= ![]() ,设函数f(x)=(x2﹣2)(x﹣x2),x∈R,若函数y=f(x)+c的图象与x轴恰有两个公共点,则实数c的取值范围是 .
,设函数f(x)=(x2﹣2)(x﹣x2),x∈R,若函数y=f(x)+c的图象与x轴恰有两个公共点,则实数c的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等腰梯形ABCD中,AB∥CD,且|AB|=2,|AD|=1,|CD|=2x其中x∈(0,1),以A,B为焦点且过点D的双曲线的离心率为e1 , 以C,D为焦点且过点A的椭圆的离心率为e2 , 若对任意x∈(0,1)不等式t<e1+e2恒成立,则t的最大值为( )
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】里氏震级M的计算公式为:M=lgA﹣lgA0 , 其中A是测震仪记录的地震曲线的最大振幅,A0是相应的标准地震的振幅,假设在一次地震中,测震仪记录的最大振幅是1000,此时标准地震的振幅A0为0.001,则此次地震的震级为级;9级地震的最大的振幅是5级地震最大振幅的倍.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1: ![]() =1(a>b>0)与双曲线C2:x2﹣
=1(a>b>0)与双曲线C2:x2﹣ ![]() =1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
=1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
A.a2= ![]()
B.a2=3
C.b2= ![]()
D.b2=2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,a∈R.
,a∈R.
(1)求f(x)的解析式;
(2)解关于x的方程f(x)=(a﹣1)4x
(3)设h(x)=2﹣xf(x), ![]() 时,对任意x1 , x2∈[﹣1,1]总有
时,对任意x1 , x2∈[﹣1,1]总有 ![]() 成立,求a的取值范围.
成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com