
分析 (1)由已知条件推导出an+1-an=(a-1)an,从而${a}_{n}=2{a}^{n-1}$,由此能求出数列{bn}的通项公式.
(2)令${b}_{n}≤\frac{3}{2}$,当n≤k时,${b}_{n}<\frac{3}{2}$,当n≥k+1时,${b}_{n}>\frac{3}{2}$,由此能求出k的值.
解答 (本小题满分13分)
解:(1)当n=1时,a2=2a,则$\frac{{a}_{2}}{{a}_{1}}=a$;
当2≤n≤2k-1时,an+1=(a-1)Sn+2,an=(a-1)Sn-1+2,
所以an+1-an=(a-1)an,故$\frac{{a}_{n+1}}{{a}_{n}}$=a,即数列{an}是等比数列,${a}_{n}=2{a}^{n-1}$,
∴Tn=a1×a2×…×an=2na1+2+…+(n-1)=${2}^{n+\frac{n(n-1)}{2k-1}}$,
bn=$\frac{1}{n}[n+\frac{n(n-1)}{2k-1}]$=$\frac{n-1}{2k-1}+1$.…(7分)
(2)令${b}_{n}≤\frac{3}{2}$,则n≤k+$\frac{1}{2}$,又n∈N*,故当n≤k时,${b}_{n}<\frac{3}{2}$,
当n≥k+1时,${b}_{n}>\frac{3}{2}$.…(8分)
|b1-$\frac{3}{2}$|+|b2-$\frac{3}{2}$|+…+|b2k-1-$\frac{3}{2}$|+|b2k-$\frac{3}{2}$|
=$(\frac{3}{2}-{b}_{1})+(\frac{3}{2}-{b}_{2})+…+({\frac{3}{2}-{b}_{k}}_{\;})$+(${b}_{k+1}-\frac{3}{2}$)+…+(${b}_{2k}-\frac{3}{2}$)…(10分)
=(k+1+…+b2k)-(b1+…+bk)
=[$\frac{\frac{1}{2}(k+2k-1)k}{2k-1}$+k]-[$\frac{\frac{1}{2}(0+k-1)k}{2k-1}+k$]
=$\frac{{k}^{2}}{2k-1}$,
由$\frac{{k}^{2}}{2k-1}≤\frac{3}{2}$,得2k2-6k+3≤0,解得$\frac{3-\sqrt{3}}{2}≤k≤\frac{3+\sqrt{3}}{2}$,…(12分)
又k≥2,且k∈N*,所以k=2.…(13分)
点评 本题考查数列的通项公式的求法,考查满足条件的实数值的求法,是中档题,解题时要认真审题,注意等比数列的性质和构造法的合理运用.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 20 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2}{7},-3$) | B. | (-2,-3) | C. | (0,$\frac{2}{7}$) | D. | (-2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 即不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
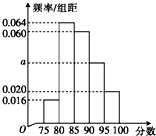 某高校在某年的自主招生考试成绩中随机抽取50名学生的笔试成绩,绘制成频率分布直方图如图所示,若要从成绩在[85,90),[90,95),[95,100]三组内的学生中,用分层抽样的方法抽取12人参加面试,则成绩在[90,100]内的学生应抽取的人数为6.
某高校在某年的自主招生考试成绩中随机抽取50名学生的笔试成绩,绘制成频率分布直方图如图所示,若要从成绩在[85,90),[90,95),[95,100]三组内的学生中,用分层抽样的方法抽取12人参加面试,则成绩在[90,100]内的学生应抽取的人数为6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com