
【题目】如图,在平面直角坐标系xOy中,A(a,0)(a>0),B(0,a),C(﹣4,0),D(0,4)设△AOB的外接圆圆心为E. 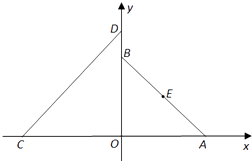
(1)若⊙E与直线CD相切,求实数a的值;
(2)设点P在圆E上,使△PCD的面积等于12的点P有且只有三个,试问这样的⊙E是否存在,若存在,求出⊙E的标准方程;若不存在,说明理由.
【答案】
(1)解:∵C(﹣4,0)、D(0,4),
∴直线CD方程为 ![]() .化简得x﹣y+4=0.
.化简得x﹣y+4=0.
又∵△AOB的外接圆圆心为E( ![]() ,
, ![]() ),半径r=
),半径r= ![]() a.
a.
∴由⊙E与直线CD相切,得圆心E到直线CD的距离等于半径,
即 ![]() =
= ![]() a,即2
a,即2 ![]() =
= ![]() a,解之得a=4
a,解之得a=4
(2)解:C(﹣4,0)、D(0,4),可得|CD|= ![]() =4
=4 ![]() ,
,
设P到直线CD的距离为d,可得△PCD的面积S= ![]() |CD|×d=12,
|CD|×d=12,
即 ![]() ,解之得d=3
,解之得d=3 ![]() .
.
因此,只须与CD平行且与CD距离为3 ![]() 的两条直线中的一条与⊙E相切,
的两条直线中的一条与⊙E相切,
另一条与⊙E相交.
∵由(1)的计算,可知圆心E到直线CD距离为2 ![]() ,
,
∴圆E的半径为2 ![]() +3
+3 ![]() =5
=5 ![]() ,即r=
,即r= ![]() a=5
a=5 ![]() ,解得a=10.
,解得a=10.
即存在a=10,满足使△PCD的面积等于12的点P有且只有三个,⊙E的标准方程是(x﹣5)2+(y﹣5)2=50.
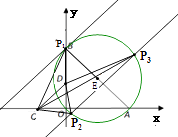
【解析】(1)根据△AOB为等腰直角三角形,算出它的圆心为E( ![]() ,
, ![]() ),半径r=
),半径r= ![]() a.求出直线CD的方程,根据⊙E与CD相切,利用点到直线的距离公式建立关于a的等式,解之即可得出实数a的值;(2)由|CD|=4
a.求出直线CD的方程,根据⊙E与CD相切,利用点到直线的距离公式建立关于a的等式,解之即可得出实数a的值;(2)由|CD|=4 ![]() 与△PCD的面积等于12,算出P到直线CD的距离为d=3
与△PCD的面积等于12,算出P到直线CD的距离为d=3 ![]() .若满足条件的点P有3个,说明与CD平行且与CD距离为3
.若满足条件的点P有3个,说明与CD平行且与CD距离为3 ![]() 的两直线中的一条与⊙E相切且另一条与⊙E相交.由此算出⊙E的半径,进而算出实数a的值,得到满足条件的⊙E的标准方程.
的两直线中的一条与⊙E相切且另一条与⊙E相交.由此算出⊙E的半径,进而算出实数a的值,得到满足条件的⊙E的标准方程.
【考点精析】解答此题的关键在于理解点到直线的距离公式的相关知识,掌握点![]() 到直线
到直线![]() 的距离为:
的距离为: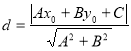 ,以及对圆的标准方程的理解,了解圆的标准方程:
,以及对圆的标准方程的理解,了解圆的标准方程:![]() ;圆心为A(a,b),半径为r的圆的方程.
;圆心为A(a,b),半径为r的圆的方程.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:
【题目】设直线l的方程是x+my+2 ![]() =0,圆O的方程是x2+y2=r2(r>0).
=0,圆O的方程是x2+y2=r2(r>0).
(1)当m取一切实数时,直线l与圆O都有公共点,求r的取值范围;
(2)r=5时,求直线l被圆O截得的弦长的取值范围;
(3)当r=1时,设圆O与x轴相交于P,Q两点,M是圆O上异于P,Q的任意一点,直线PM交直线l′:x=3于点P′,直线QM交直线l′于点Q′.求证:以P′Q′为直径的圆C总经过定点,并求出定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,侧面PAB⊥底面ABCD.若PA=AD=AB=kBC(0<k<1),则( ) 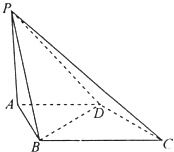
A.当k= ![]() 时,平面BPC⊥平面PCD
时,平面BPC⊥平面PCD
B.当k= ![]() 时,平面APD⊥平面PCD
时,平面APD⊥平面PCD
C.对?k∈(0,1),直线PA与底面ABCD都不垂直
D.?k∈(0,1),使直线PD与直线AC垂直.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( ) 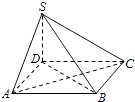
A.AC⊥SB
B.AB∥平面SCD
C.SA与平面SBD所成的角等于SC与平面SBD所成的角
D.AB与SC所成的角等于DC与SA所成的角
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D. 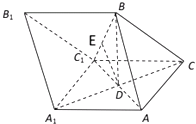
(1)求证:BD⊥A1C;
(2)若E在棱BC1上,且满足DE∥面ABC,求三棱锥E﹣ACC1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以O为极点,x轴的正半轴为极轴的极坐标系中,直线l的极坐标方程为θ= ![]() ,曲线C的参数方程为
,曲线C的参数方程为 ![]() .
.
(1)写出直线l与曲线C的直角坐标方程;
(2)过点M平行于直线l1的直线与曲线C交于A、B两点,若|MA||MB|= ![]() ,求点M轨迹的直角坐标方程.
,求点M轨迹的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A,B,C,D为空间四点.在△ABC中,AB=2,AC=BC= ![]() .等边三角形ADB以AB为轴运动.
.等边三角形ADB以AB为轴运动. 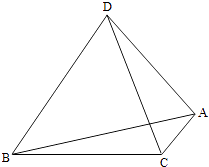
(1)当平面ADB⊥平面ABC时,求CD;
(2)当△ADB转动时,是否总有AB⊥CD?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com