
【题目】已知函数![]() 为定义域R上的奇函数,且在R上是单调递增函数,函数
为定义域R上的奇函数,且在R上是单调递增函数,函数![]() ,数列
,数列![]() 为等差数列,且公差不为0,若
为等差数列,且公差不为0,若![]() ,则
,则![]() ( )
( )
A. 45B. 15C. 10D. 0
【答案】A
【解析】
根据题意,由奇函数的性质可得(-x)+f(x)=0,又由g(x)=f(x-5)+x且g(a1)+g(a2)+…+g(a9)=45,可得f(a1-5)+f(a2-5)+…+f(a9-5)+(a1+a2+…+a9)=45,结合等差数列的性质可得f(a1-5)=-f(a9-5)=f(5-a9),进而可得a1-5=5-a9,即a1+a9=10,进而计算可得答案.
根据题意,函数y=f(x)为定义域R上的奇函数,
则有f(-x)+f(x)=0,
∵g(x)=f(x-5)+x,
∴若g(a1)+g(a2)+…+g(a9)=45,
即f(a1-5)+a1+f(a2-5)+a2+…+f(a9-5)+a9=45,
即f(a1-5)+f(a2-5)+…+f(a9-5)+(a1+a2+…+a9)=45,
f(a1-5)+f(a2-5)+…+f(a9-5)=0,
又由y=f(x)为定义域R上的奇函数,
则f(a1-5)+f(a9-5)=0,
即f(a1-5)=-f(a9-5)=f(5-a9),
∵f(x)在R上是单调函数,
∴a1-5=5-a9,
即a1+a9=10,
在等差数列中,a1+a9=10=2a5,
即a5=5,
则a1+a2+…+a9=9a5=45;
故选:A.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,离心率
,离心率![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 且不与坐标轴垂直的直线交椭圆
且不与坐标轴垂直的直线交椭圆![]() 于
于![]() 、
、![]() 两点,线段
两点,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求点
,求点![]() 的横坐标的取值范围;
的横坐标的取值范围;
(3)在第(2)问的条件下,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知椭圆![]() :
:![]() 的焦距为
的焦距为![]() ,离心率为
,离心率为![]() ,其右焦点为
,其右焦点为![]() ,过点
,过点![]() 作直线交椭圆于另一点
作直线交椭圆于另一点![]() .
.
(1)若![]() ,求
,求![]() 外接圆的方程;
外接圆的方程;
(2)若过点![]() 的直线与椭圆
的直线与椭圆![]()
![]() 相交于两点
相交于两点![]() 、
、![]() ,设
,设![]() 为
为![]() 上一点,且满足
上一点,且满足![]() (
(![]() 为坐标原点),当
为坐标原点),当![]() 时,求实数
时,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两次购买同一种物品,可以用两种不同的策略,第一种是不考虑物品价格的升降,每次购买这种物品的数量一定;第二种是不考虑物品价格的升降,每次购买这种物品所花的钱数一定.哪种购物方式比较经济?你能把所得结论作一些推广吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高一年级学生中随机抽取了20名学生,将他们的数学检测成绩(分)分成六段(满分100分,成绩均为不低于40分的整数):![]() ,
,![]() ,...,
,...,![]() 后,得到如图所示的频率分布直方图.
后,得到如图所示的频率分布直方图.
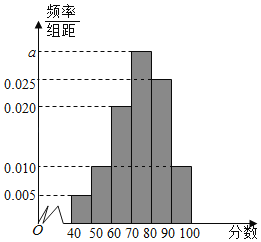
(Ⅰ)求图中实数![]() 的值;
的值;
(Ⅱ)若该校高一年级共有学生600名,试根据以上数据,估计该校高一年级数学检测成绩不低于80分的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点F(1,0),O为坐标原点,A,B是抛物线C上异于 O的两点.
的焦点F(1,0),O为坐标原点,A,B是抛物线C上异于 O的两点.
(1)求抛物线C的方程;
(2)若直线AB过点(8,0),求证:直线OA,OB的斜率之积为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
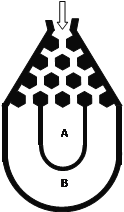
【题目】(本题满分12分)将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中,将3次遇到黑色障碍物,最后落入![]() 袋或
袋或![]() 袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是.
袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是.
(Ⅰ)求小球落入![]() 袋中的概率
袋中的概率![]() ;
;
(Ⅱ)在容器入口处依次放入4个小球,记![]() 为落入
为落入![]() 袋中小球的个数,试求
袋中小球的个数,试求![]() 的概率和
的概率和![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com