
【题目】已知抛物线![]() ,直线
,直线![]() (
(![]() )与
)与![]() 交于
交于![]() 两点,
两点,![]() 为
为![]() 的中点,
的中点,![]() 为坐标原点.
为坐标原点.
(1)求直线![]() 斜率的最大值;
斜率的最大值;
(2)若点![]() 在直线
在直线![]() 上,且
上,且![]() 为等边三角形,求点
为等边三角形,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
解法一:(1)设![]() 两点坐标,将直线方程与抛物线方程联立,根据一元二次方程根与系数关系、根的判别式、中点坐标公式求出
两点坐标,将直线方程与抛物线方程联立,根据一元二次方程根与系数关系、根的判别式、中点坐标公式求出![]() 的坐标,最后根据斜率公式,结合基本不等式进行求解即可;
的坐标,最后根据斜率公式,结合基本不等式进行求解即可;
(2)利用弦长公式求出等边三角形的边长,最后利用等边三角形的性质,得到方程,求解方程即可求出点![]() 的坐标.
的坐标.
解法二:(1)设出![]() 两点的坐标,根据点在抛物线上,得到两个方程,再利用
两点的坐标,根据点在抛物线上,得到两个方程,再利用![]() 两点在直线上、中点坐标公式求出
两点在直线上、中点坐标公式求出![]() 的坐标,最后根据斜率公式,结合基本不等式进行求解即可;
的坐标,最后根据斜率公式,结合基本不等式进行求解即可;
(2)将直线方程与抛物线方程联立,根据一元二次方程根与系数关系、根的判别式、两点间距离公式求出等边三角形的边长,最后利用等边三角形的性质,得到方程,求解方程即可求出点![]() 的坐标.
的坐标.
解法一:(1)设![]() ,
,
由![]() ,消去
,消去![]() 得,
得,![]() ,
,
![]() 且
且![]() .
.
所以![]()
因为![]() 为
为![]() 的中点,
的中点,
所以![]() 的坐标为
的坐标为![]() ,即
,即![]() ,
,
又因为![]() ,所以
,所以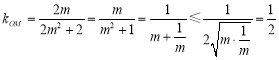 ,
,
(当且仅当![]() ,即
,即![]() 等号成立.)
等号成立.)
所以![]() 的斜率的最大值为
的斜率的最大值为![]() ;
;
(2)由(1)知,
![]()
![]()
![]()
![]() ,
,
由![]() 得
得![]() ,
,
因为![]() 为等边三角形,所以
为等边三角形,所以![]() ,
,
所以![]() ,
,
所以![]() ,所以
,所以![]() ,解得
,解得![]()
又![]() ,所以
,所以![]() ,
,
则![]() ,直线
,直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
所以![]() 时,
时,![]() ,
,
所以所求的点![]() 的坐标为
的坐标为![]() .
.
解法二:(1)设![]() ,
,
因为![]() 为
为![]() 的中点,且直线
的中点,且直线![]() ,
,
所以![]() 因为
因为![]() ,
,![]() ,两个等式相减得:
,两个等式相减得:![]()
由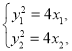 得
得![]()
所以![]() 所以
所以![]() 即
即![]() .
.
所以![]() 即
即![]() ,
,
又因为![]() ,所以
,所以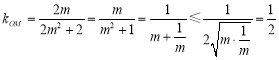 ,
,
(当且仅当![]() ,即
,即![]() 等号成立.)
等号成立.)
所以![]() 的斜率的最大值为
的斜率的最大值为![]() .
.
(2)由![]() ,消去
,消去![]() 得
得![]() ,
,
所以![]() 且
且![]() .
.
![]()
![]()
![]()
![]()
![]() ,
,
由(1)知,![]() 的中点
的中点![]() 的坐标为
的坐标为![]() ,
,
所以线段![]() 的垂直平分线方程为:
的垂直平分线方程为:![]() .
.
令![]() ,得线段
,得线段![]() 的垂直平分线与直线
的垂直平分线与直线![]() 交点坐标为
交点坐标为![]()
所以![]() .
.
因为![]() 为等边三角形,所以
为等边三角形,所以![]() ,
,
所以![]() ,
,
所以![]() ,所以
,所以![]() ,解得
,解得![]()
因为![]() 所以
所以![]() ,
,
则![]() ,直线
,直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
所以![]() 时,
时,![]() ,
,
所以所求的点![]() 的坐标为
的坐标为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,等腰直角三角形ABC所在的平面与半圆弧AB所在的平面垂直,AC⊥AB,P是弧AB上一点,且∠PAB=30°.
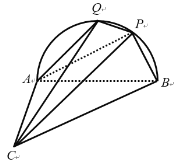
(1)证明:平面BCP⊥平面ACP;
(2)若Q是弧AP上异于AP的一个动点,当三棱锥C-APQ体积最大时,求二面角A-PQ-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点.对任意的点
为坐标原点.对任意的点![]() ,定义
,定义![]() .任取点
.任取点![]() ,
,![]() ,记
,记![]() ,
,![]() ,若此时
,若此时![]() 成立,则称点
成立,则称点![]() ,
,![]() 相关.
相关.
(1)分别判断下面各组中两点是否相关,并说明理由;
①![]() ,
,![]() ;②
;②![]() ,
,![]() .
.
(2)给定![]() ,
,![]() ,点集
,点集![]() .
.
(![]() )求集合
)求集合![]() 中与点
中与点![]() 相关的点的个数;
相关的点的个数;
(![]() )若
)若![]() ,且对于任意的
,且对于任意的![]() ,
,![]() ,点
,点![]() ,
,![]() 相关,求
相关,求![]() 中元素个数的最大值.
中元素个数的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年2月,全国掀起了“停课不停学”的热潮,各地教师通过网络直播、微课推送等多种方式来指导学生线上学习.为了调查学生对网络课程的热爱程度,研究人员随机调查了相同数量的男、女学生,发现有![]() 的男生喜欢网络课程,有
的男生喜欢网络课程,有![]() 的女生不喜欢网络课程,且有
的女生不喜欢网络课程,且有![]() 的把握但没有
的把握但没有![]() 的把握认为是否喜欢网络课程与性别有关,则被调查的男、女学生总数量可能为( )
的把握认为是否喜欢网络课程与性别有关,则被调查的男、女学生总数量可能为( )
附: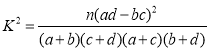 ,其中
,其中![]() .
.
|
|
|
|
|
k |
|
|
|
|
A.130B.190C.240D.250
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 对任意的
对任意的![]() 都有
都有![]() ,且
,且![]() 时
时![]() 的最大值为
的最大值为![]() ,下列四个结论:①
,下列四个结论:①![]() 是
是![]() 的一个极值点;②若
的一个极值点;②若![]() 为奇函数,则
为奇函数,则![]() 的最小正周期
的最小正周期![]() ;③若
;③若![]() 为偶函数,则
为偶函数,则![]() 在
在![]() 上单调递增;④
上单调递增;④![]() 的取值范围是
的取值范围是![]() .其中一定正确的结论编号是( )
.其中一定正确的结论编号是( )
A.①②B.①③C.①②④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱柱![]() 中,已知底面
中,已知底面![]() 为等腰梯形,
为等腰梯形,![]() ,
,![]() ,M,N分别是棱
,M,N分别是棱![]() ,
,![]() 的中点
的中点
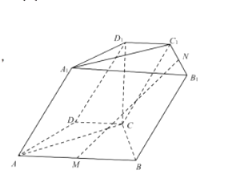
(1)证明:直线![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,且
,且![]() ,求经过点A,M,N的平面
,求经过点A,M,N的平面![]() 与平面
与平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com