Question

5．椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞0，b＞0）$的左焦点为F，A（-a，0），B（0，b），C（0，-b）分别为其三个顶点．直线CF与AB交于点D，若椭圆的离心率$e=\frac{1}{2}$，则tan∠BDC=$-3\sqrt{3}$．

Answer 1

分析 由椭圆的离心率得到a，b，c之间的关系，利用这些关系表示出∠BAO、∠CFO的正切值，由图得∠BDC=∠BAO+∠CFO，利用两角和的正切求出tan∠BDC的值．

解答 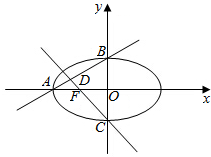解：由题意得离心率e=$\frac{c}{a}=\frac{1}{2}$，则设c=m，a=2m（m＞0），
由a²=b²+c²得，b²=a²-c²=3m²，解得b=$\sqrt{3}m$，
由图可知，∠DFA=∠CFO，且∠BDC=∠BAO+∠DFA，
∴∠BDC=∠BAO+∠CFO，
又tan∠BAO=$\frac{OB}{OA}=\frac{b}{a}$=$\frac{\sqrt{3}}{2}$，tan∠CFO=$\frac{OC}{OF}=\frac{b}{c}=\sqrt{3}$，
则tan∠BDC=tan（∠BAO+∠OFC）=$\frac{tan∠BAO+tan∠CFO}{1-tan∠BAOtan∠CFO}$=$\frac{\frac{\sqrt{3}}{2}+\sqrt{3}}{1-\frac{\sqrt{3}}{2}×\sqrt{3}}=-3\sqrt{3}$．
故答案为：$-3\sqrt{3}$．

点评 本题考查椭圆的简单性质的应用，考查两角和与差的正切函数，训练了平面几何在解圆锥曲线问题中的应用，是中档题．