
【题目】已知函数f(x)与函数g(x)的图像关于原点对称,且f(x)=![]() +2x, 若函数F(x)=g(x)-
+2x, 若函数F(x)=g(x)-![]() f(x)+1在区间
f(x)+1在区间![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围。
的取值范围。
【答案】(-![]() ,0]
,0]
【解析】
由函数f(x)与函数g(x)的图像关于原点对称,且f(x)=![]() +2x即可求得g(x)=-
+2x即可求得g(x)=-![]() +2x,从而求得:F(x)=-(1+
+2x,从而求得:F(x)=-(1+![]() )
)![]() +2(1-
+2(1-![]() )x+1,对
)x+1,对![]() 的范围分类即可求得使F(x)在区间
的范围分类即可求得使F(x)在区间![]() 上是增函数的实数
上是增函数的实数![]() 的取值范围.
的取值范围.
由题意知,g(x)=-f(-x)=-![]() +2x,则F(x)=-(1+
+2x,则F(x)=-(1+![]() )
)![]() +2(1-
+2(1-![]() )x+1.
)x+1.
当1+![]() =0,即
=0,即![]() =-1时,F(x)=4x+1在区间
=-1时,F(x)=4x+1在区间![]() 上是增函数,从而
上是增函数,从而![]() =-1;
=-1;
当1+![]() 〉0,即
〉0,即![]() 〉-1时,若F(x)在区间
〉-1时,若F(x)在区间![]() 上是增函数,则
上是增函数,则![]() ,解得-1<
,解得-1<![]()
![]() 0;
0;
当1+![]() < 0,即
< 0,即![]() <-1时,若F(x)在区间
<-1时,若F(x)在区间![]() 上是增函数,则
上是增函数,则![]() 显然成立,从而
显然成立,从而![]() <-1;
<-1;
综上所述,实数![]() 的取值范围为(-
的取值范围为(-![]() ,0]。
,0]。


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
【题目】(2017·金华调研)如图,AB=BE=BC=2AD=2,且AB⊥BE,∠DAB=60°,AD∥BC,BE⊥AD.
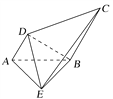
(1)求证:平面ADE⊥平面BDE;
(2)求直线AD与平面DCE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,曲线![]() 的普通方程为
的普通方程为![]() ,以原点为极点,
,以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,并取与直角坐标系相同的长度单位,建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,并取与直角坐标系相同的长度单位,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 、
、![]() 的参数方程;
的参数方程;
(Ⅱ)若点![]() 、
、![]() 分别在曲线
分别在曲线![]() 、
、![]() 上,求
上,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司想了解对某产品投入的宣传费用与该产品的营业额的影响.下面是以往公司对该产品的宣传费用![]() (单位:万元)和产品营业额
(单位:万元)和产品营业额![]() (单位:万元)的统计折线图.
(单位:万元)的统计折线图.

(Ⅰ)根据折线图可以判断,可用线性回归模型拟合宣传费用![]() 与产品营业额
与产品营业额![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(Ⅱ)建立产品营业额![]() 关于宣传费用
关于宣传费用![]() 的归方程;
的归方程;
(Ⅲ)若某段时间内产品利润![]() 与宣传费
与宣传费![]() 和营业额
和营业额![]() 的关系为
的关系为![]() ,应投入宣传费多少万元才能使利润最大,并求最大利润.
,应投入宣传费多少万元才能使利润最大,并求最大利润.
参考数据: ![]() ,
, ![]() ,
, ![]() ,
, 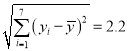 ,
, ![]()
参考公式:相关系数, 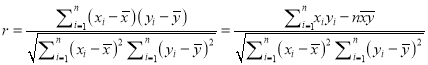 ,
,
回归方程![]() 中斜率和截距的最小二乘佔计公式分别为
中斜率和截距的最小二乘佔计公式分别为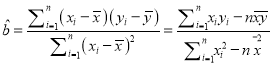 ,
, ![]() .(计算结果保留两位小数)
.(计算结果保留两位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市交通部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照![]() ,
,![]() ,
,![]() ,
,![]() 分成5组,制成如图所示频率分直方图.
分成5组,制成如图所示频率分直方图.

(1)求图中x的值;
(2)求这组数据的平均数和中位数;
(3)已知满意度评分值在![]() 内的男生数与女生数的比为
内的男生数与女生数的比为![]() ,若在满意度评分值为
,若在满意度评分值为![]() 的人中随机抽取2人进行座谈,求2人均为男生的概率.
的人中随机抽取2人进行座谈,求2人均为男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() 是集合
是集合![]()
![]() 的一个含有
的一个含有![]() 个元素的子集.
个元素的子集.
(Ⅰ)当![]() 时,
时,
设![]()
(i)写出方程![]() 的解
的解![]() ;
;
(ii)若方程![]() 至少有三组不同的解,写出
至少有三组不同的解,写出![]() 的所有可能取值.
的所有可能取值.
(Ⅱ)证明:对任意一个![]() ,存在正整数
,存在正整数![]() 使得方程
使得方程![]()
![]() 至少有三组不同的解.
至少有三组不同的解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com