
设函数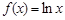 ,
,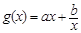 ,函数
,函数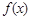 的图象与
的图象与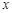 轴的交点也在函数
轴的交点也在函数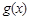 的图象上,且在此点有公切线.
的图象上,且在此点有公切线.
(Ⅰ)求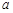 ,
,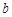 的值;
的值;
(Ⅱ)试比较 与
与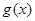 的大小.
的大小.
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:解答题
某商场销售某种商品的经验表明,该商品每日的销售量 (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式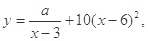 其中
其中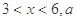 为常数.己知销售价格为5元/千克时,每日可售出该商品11千克.
为常数.己知销售价格为5元/千克时,每日可售出该商品11千克.
(1)求 的值;
的值;
(2)若该商品的成本为3元/千克,试确定销售价格 的值,使商场每日销售该商品所获得利润最大.
的值,使商场每日销售该商品所获得利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数
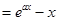 ,其中
,其中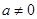 .
.
(1)若对一切x∈R, ≥1恒成立,求a的取值集合;
≥1恒成立,求a的取值集合;
(2)在函数 的图像上取定两点
的图像上取定两点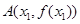 ,
,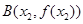
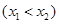 ,记直线AB的斜率 为k,问:是否存在x0∈(x1,x2),使
,记直线AB的斜率 为k,问:是否存在x0∈(x1,x2),使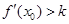 成立?若存在,求
成立?若存在,求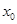 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com