
【题目】已知直线![]() 的斜率为
的斜率为![]() ,纵截距为
,纵截距为![]() .
.
(1)求点(2,4)关于直线![]() 的对称点坐标;
的对称点坐标;
(2)求与直线![]() 平行且距离为
平行且距离为![]() 的直线方程.
的直线方程.
【答案】(1)![]() ; (2)
; (2)![]() 或
或![]()
【解析】
(1)设点![]() 为
为![]() ,则
,则![]() 关于直线
关于直线![]() 的对称点坐标为
的对称点坐标为![]()
![]() ,利用点关于直线对称的性质,以及中垂线定理,列出关于
,利用点关于直线对称的性质,以及中垂线定理,列出关于![]() 的式子,结合
的式子,结合![]() 的中点
的中点![]() 在直线
在直线![]() 上,即可求出
上,即可求出![]() 和
和![]() ;
;
(2)根据平行直线系方程,由已知直线![]() 写出与它平行的直线
写出与它平行的直线![]() 的方程为:
的方程为:![]() ,再利用两平行线间的距离公式,求出
,再利用两平行线间的距离公式,求出![]() ,即可得出直线方程.
,即可得出直线方程.
已知直线![]() 的斜率为
的斜率为![]() ,纵截距为
,纵截距为![]() ,则方程为:
,则方程为:![]() ,
,
(1)设点![]() 为点
为点![]() ,则
,则![]() 关于直线
关于直线![]() 的对称点坐标为
的对称点坐标为![]()
![]() ,
,
则直线![]() 与直线
与直线![]() 垂直,则
垂直,则![]() ,即
,即![]() ①,
①,
且![]() 的中点
的中点![]() 在直线
在直线![]() 上,所以
上,所以![]() ②,
②,
联立①和②,解得![]() ,
,
所以点![]() 关于直线
关于直线![]() 的对称点坐标为
的对称点坐标为![]() .
.
(2)设所求的直线为![]() ,因为直线
,因为直线![]() 与直线
与直线![]() 平行且距离为
平行且距离为![]() ,
,
又因为直线![]() 方程为:
方程为:![]() ,即
,即![]() ,
,
所以可设直线![]() 的方程为:
的方程为:![]() ,
,
则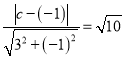 ,解得
,解得![]() 或-11.
或-11.
所以直线![]() 的方程为:
的方程为:![]() 或
或![]() .
.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】现有![]() 个小球,甲、乙两位同学轮流且不放回抓球,每次最少抓1个球,最多抓3个球,规定谁抓到最后一个球谁赢. 如果甲先抓,那么下列推断正确的是( )
个小球,甲、乙两位同学轮流且不放回抓球,每次最少抓1个球,最多抓3个球,规定谁抓到最后一个球谁赢. 如果甲先抓,那么下列推断正确的是( )
A. 若![]() =4,则甲有必赢的策略 B. 若
=4,则甲有必赢的策略 B. 若![]() =6,则乙有必赢的策略
=6,则乙有必赢的策略
C. 若![]() =9,则甲有必赢的策略 D. 若
=9,则甲有必赢的策略 D. 若![]() =11,则乙有必赢的策略
=11,则乙有必赢的策略
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的产品中分正品与次品,正品重![]() ,次品重
,次品重![]() ,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第
,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第![]() 袋取出
袋取出![]() 个产品(
个产品(![]() ),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量
),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量![]() ,若次品所在的袋子的编号是2,此时的重量
,若次品所在的袋子的编号是2,此时的重量![]() _________
_________![]() ;若次品所在的袋子的编号是
;若次品所在的袋子的编号是![]() ,此时的重量
,此时的重量![]() _______
_______![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】噪声污染已经成为影响人们身体健康和生活质量的严重问题,为了了解强度![]() (单位:分贝)与声音能量
(单位:分贝)与声音能量![]() (单位:
(单位:![]() )之间的关系,将测量得到的声音强度
)之间的关系,将测量得到的声音强度![]() 和声音能量
和声音能量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.

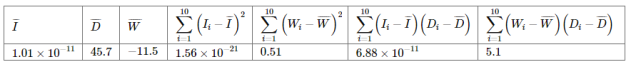
表中![]() ,
,![]()
(1)根据表中数据,求声音强度![]() 关于声音能量
关于声音能量![]() 的回归方程
的回归方程![]() ;
;
(2)当声音强度大于60分贝时属于噪音,会产生噪声污染,城市中某点![]() 共受到两个声源的影响,这两个声源的声音能量分别是
共受到两个声源的影响,这两个声源的声音能量分别是![]() 和
和![]() ,且
,且![]() .已知点
.已知点![]() 的声音能量等于声音能量
的声音能量等于声音能量![]() 与
与![]() 之和.请根据(1)中的回归方程,判断
之和.请根据(1)中的回归方程,判断![]() 点是否受到噪声污染的干扰,并说明理由.
点是否受到噪声污染的干扰,并说明理由.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: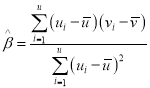 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 的底面ABCD为菱形,
的底面ABCD为菱形,![]() ,侧面PAD与底面ABCD所成的角为
,侧面PAD与底面ABCD所成的角为![]() ,
,![]() 是等边三角形,点P到平面ABCD距离为
是等边三角形,点P到平面ABCD距离为![]() .
.
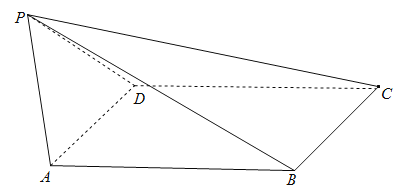
(1)证明:![]() ;
;
(2)求二面角![]() 余弦值.
余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自由购是一种通过自助结算购物的形式.某大型超市为调查顾客自由购的使用情况,随机抽取了100人,调查结果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(1)现随机抽取1名顾客,试估计该顾客年龄在[30,50)且未使用自由购的概率;
(2)从被抽取的年龄在[50,70]使用的自由购顾客中,随机抽取2人进一步了解情况,求这2人年龄都在[50,60)的概率;
(3)为鼓励顾客使用自由购,该超市拟对使用自由购顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com