
【题目】已知函数![]() (
(![]() ,
,![]() 为自然对数的底数).
为自然对数的底数).
(1)若![]() ,求函数
,求函数![]() 的图像在点
的图像在点![]() 处的切线方程;
处的切线方程;
(2)![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的右准线为直线
的右准线为直线![]() ,左顶点为
,左顶点为![]() ,右焦点为
,右焦点为![]() . 已知斜率为2的直线
. 已知斜率为2的直线![]() 经过点
经过点![]() ,与椭圆
,与椭圆![]() 相交于
相交于![]() 两点,且
两点,且![]() 到直线
到直线![]() 的距离为
的距离为![]()
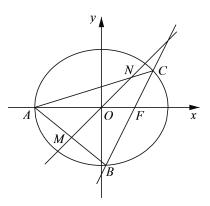
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过![]() 的直线
的直线![]() 与直线
与直线![]() 分别相交于
分别相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机调查某城市80名有子女在读小学的成年人,以研究晚上八点至十点时间段辅导子女作业与性别的关系,得到下面的数据表:
是否辅导 性别 | 辅导 | 不辅导 | 合计 |
男 | 25 | 60 | |
女 | |||
合计 | 40 | 80 |
(1)请将表中数据补充完整;
(2)用样本的频率估计总体的概率,估计这个城市有子女在读小学的成人女性晚上八点至十点辅导子女作业的概率;
(3)根据以上数据,能否有99%以上的把握认为“晚上八点至十点时间段是否辅导子女作业与性别有关?”.
参考公式: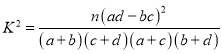 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年新型冠状病毒疫情爆发,贵州省教育厅号召全体学生“停课不停学”.自
年新型冠状病毒疫情爆发,贵州省教育厅号召全体学生“停课不停学”.自![]() 月
月![]() 日起,高三年级学生通过收看“阳光校园·空中黔课”进行线上网络学习.为了检测线上网络学习效果,某中学随机抽取
日起,高三年级学生通过收看“阳光校园·空中黔课”进行线上网络学习.为了检测线上网络学习效果,某中学随机抽取![]() 名高三年级学生做“是否准时提交作业”的问卷调查,并组织了一场线上测试,调查发现有
名高三年级学生做“是否准时提交作业”的问卷调查,并组织了一场线上测试,调查发现有![]() 名学生每天准时提交作业,根据他们的线上测试成绩得频率分布直方图(如图
名学生每天准时提交作业,根据他们的线上测试成绩得频率分布直方图(如图![]() 所示);另外
所示);另外![]() 名学生偶尔没有准时提交作业,根据他们的线上测试成绩得茎叶图(如图
名学生偶尔没有准时提交作业,根据他们的线上测试成绩得茎叶图(如图![]() 所示,单位:分)
所示,单位:分)
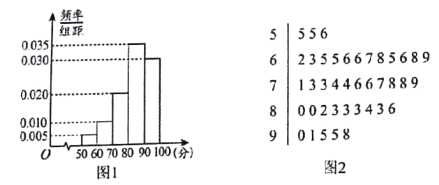
(1)成绩不低于![]() 分为
分为![]() 等,低于
等,低于![]() 分为非
分为非![]() 等.完成以下列联表,并判断是否有
等.完成以下列联表,并判断是否有![]() 以上的把握认为成绩取得
以上的把握认为成绩取得![]() 等与每天准时提交作业有关?
等与每天准时提交作业有关?
准时提交作业与成绩等次列联表 | 单位:人 | ||
A等 | 非A等 | 合计 | |
每天准时提交作业 | |||
偶尔没有准时提交作业 | |||
合计 | |||
(2)成绩低于![]() 分为不合格,从这
分为不合格,从这![]() 名学生里成绩不合格的学生中再抽取
名学生里成绩不合格的学生中再抽取![]() 人,其中每天准时提交作业的学生人数为
人,其中每天准时提交作业的学生人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附: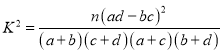
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读下列材料,回答所提问题:设函数![]() ,①
,①![]() 的定义域为
的定义域为![]() ,其图像是一条连续不断的曲线;②
,其图像是一条连续不断的曲线;②![]() 是偶函数;③
是偶函数;③![]() 在
在![]() 上不是单调函数;④
上不是单调函数;④![]() 恰有
恰有![]() 个零点,写出符合上述①②④条件的一个函数的解析式是______;写出符合上述所有条件的一个函数的解析式是______.
个零点,写出符合上述①②④条件的一个函数的解析式是______;写出符合上述所有条件的一个函数的解析式是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】羽毛球比赛中,首局比赛由裁判员采用抛球的方法决定谁先发球,在每回合争夺中,赢方得1分且获得发球权.每一局中,获胜规则如下:①率先得到21分的一方赢得该局比赛;②如果双方得分出现![]() ,需要领先对方2分才算该局获胜;③如果双方得分出现
,需要领先对方2分才算该局获胜;③如果双方得分出现![]() ,先取得30分的一方该局获胜.现甲、乙两名运动员进行对抗赛,在每回合争夺中,若甲发球时,甲得分的概率为
,先取得30分的一方该局获胜.现甲、乙两名运动员进行对抗赛,在每回合争夺中,若甲发球时,甲得分的概率为![]() ;乙发球时,甲得分的概率为
;乙发球时,甲得分的概率为![]() .
.
(Ⅰ)若![]() ,记“甲以
,记“甲以![]() 赢一局”的概率为
赢一局”的概率为![]() ,试比较
,试比较![]() 与
与![]() 的大小;
的大小;
(Ⅱ)根据对以往甲、乙两名运动员的比赛进行数据分析,得到如下![]() 列联表部分数据.若不考虑其它因素对比赛的影响,并以表中两人发球时甲得分的频率作为
列联表部分数据.若不考虑其它因素对比赛的影响,并以表中两人发球时甲得分的频率作为![]() ,
,![]() 的值.
的值.
甲得分 | 乙得分 | 总计 | |
甲发球 | 50 | 100 | |
乙发球 | 60 | 90 | |
总计 | 190 |
①完成![]() 列联表,并判断是否有95%的把握认为“比赛得分与接、发球有关”?
列联表,并判断是否有95%的把握认为“比赛得分与接、发球有关”?
②已知在某局比中,双方战成![]() ,且轮到乙发球,记双方再战
,且轮到乙发球,记双方再战![]() 回合此局比赛结束,求
回合此局比赛结束,求![]() 的分布列与期望.
的分布列与期望.
参考公式: ,其中
,其中![]() .
.
临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C的对边长分别等于a,b,c,列举如下五个条件:①![]() ;②
;②![]() ;③cosA+cos2A=0;④a=4;⑤△ABC的面积等于
;③cosA+cos2A=0;④a=4;⑤△ABC的面积等于![]() .
.
(1)请在五个条件中选择一个(只需选择一个)能够确定角A大小的条件来求角A;
(2)在(1)的结论的基础上,再在所给条件中选择一个(只需选择一个),求△ABC周长的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com