
【题目】已知函数![]() ,函数
,函数![]() .
.
![]() Ⅰ
Ⅰ![]() 若函数
若函数![]() 在
在![]() 和
和![]() 上单调性相反,求
上单调性相反,求![]() 的解析式;
的解析式;
![]() Ⅱ
Ⅱ![]() 若
若![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求a的取值范围;
上恒成立,求a的取值范围;
![]() Ⅲ
Ⅲ![]() 已知
已知![]() ,若函数
,若函数![]() 在区间
在区间![]() 内有且只有一个零点,试确定实数a的范围.
内有且只有一个零点,试确定实数a的范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
![]() Ⅰ
Ⅰ![]() 若函数
若函数![]() 在
在![]() 和
和![]() 上单调性相反,得到
上单调性相反,得到![]() 是对称轴,进行求解即可求
是对称轴,进行求解即可求![]() 的分析式;
的分析式;
![]() Ⅱ
Ⅱ![]() 利用参数分离法将不等式
利用参数分离法将不等式![]() 在
在![]() 上恒成立转化为求最值问题即可,求a的取值范围;
上恒成立转化为求最值问题即可,求a的取值范围;
![]() Ⅲ
Ⅲ![]() 根据函数零点和方程之间的关系,判断函数的单调性,即可得到结论.
根据函数零点和方程之间的关系,判断函数的单调性,即可得到结论.
![]() Ⅰ
Ⅰ![]() 由单调性知,函数
由单调性知,函数![]() 为二次函数,
为二次函数,
其对称轴为![]() ,解得
,解得![]() ,
,
![]() 所求
所求![]()
![]() Ⅱ
Ⅱ![]() 依题意得
依题意得![]() ,
,
即![]() 在
在![]() 上恒成立,
上恒成立,
转化为![]() 在
在![]() 上恒成立,
上恒成立,
![]() 在
在![]() 上恒成立,
上恒成立,
转化为![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,则转化为
,则转化为![]() 在
在![]() 上恒成立
上恒成立
即![]() ,
,![]() 所以
所以![]()
![]() Ⅲ
Ⅲ![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,
则原命题等价于两个函数![]() 与
与![]() 的图象在区间
的图象在区间![]() 内有唯一交点.
内有唯一交点.
当![]() 时,
时,![]() 在
在![]() 内为减函数,
内为减函数,![]() ,
,![]() 为增函数,
为增函数,
且![]() ,
,![]() ,
,![]() 函数在区间有唯一的交点;
函数在区间有唯一的交点;
当![]() 时,
时,![]() 图象开口向下,对称轴为
图象开口向下,对称轴为![]() ,
,
![]() 在
在![]() 内为减函数,
内为减函数,![]() ,
,![]() 为增函数,
为增函数,
且![]() ,
,
![]() .
.
当![]() 时,
时,![]() 图象开口向上,对称轴为
图象开口向上,对称轴为![]() ,
,
![]() 在
在![]() 内为减函数,
内为减函数,![]() ,
,![]() 为增函数,
为增函数,
则由![]() ,
,
![]() .
.
综上,所求a的取值范围为![]()


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】袋中装有一些大小相同的小球,其中号数为1的小球1个,号数为2的小球2个,号数为3的小球3个,…,号数为n的小球有n个,从袋中取一球,其号数记为随机变量![]() ,则
,则![]() 的数学期望E
的数学期望E![]() =______________.
=______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图在棱长均为2的正四棱锥P﹣ABCD中,点E为PC中点,则下列命题正确的是( ) 
A.BE平行面PAD,且直线BE到面PAD距离为 ![]()
B.BE平行面PAD,且直线BE到面PAD距离为 ![]()
C.BE不平行面PAD,且BE与平面PAD所成角大于 ![]()
D.BE不平行面PAD,且BE与面PAD所成角小于 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直角三角形ABC中,A=60°,沿斜边AC上的高BD,将△ABD折起到△PBD的位置,点E在线段CD上.
(1)求证:PE⊥BD;
(2)过点D作DM⊥BC交BC于点M,点N为PB中点,若PE∥平面DMN,求 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人在相同条件下各打靶10次,每次打靶所得的环数如图所示.
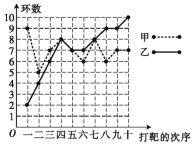
填写下表,请从下列角度对这次结果进行分析.
命中9环及以上的次数 | 平均数 | 中位数 | 方差 | |
甲 | ||||
乙 |
(1)命中9环及以上的次数(分析谁的成绩好些);
(2)平均数和中位数(分析谁的成绩好些);
(3)方差(分析谁的成绩更稳定);
(4)折线图上两人射击命中环数的走势(分析谁更有潜力).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 ,(
,(![]() 为参数),圆
为参数),圆![]() 的标准方程为
的标准方程为![]() .以坐标原点为极点,
.以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求直线![]() 和圆
和圆![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() 与的交点为
与的交点为![]() ,与圆
,与圆![]() 的交点为
的交点为![]() ,且点
,且点![]() 恰好为线段
恰好为线段![]() 的中点,求
的中点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com