
| A.15 | B.18 |
| C.19 | D.23 |
科目:高中数学 来源:不详 题型:解答题
| 表1 | 表2 | 表3 | … |
| 1 | 1 3 | 1 3 5 | |
| | 4 | 4 8 | |
| | | 12 | |
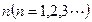 有
有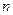 行,第1行的
行,第1行的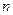 个数
个数 是1,3,5,…,
是1,3,5,…,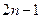 ,从第2行起,每行中的每个数都等于它肩上的两数之和。
,从第2行起,每行中的每个数都等于它肩上的两数之和。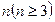 (不要求证明)
(不要求证明)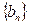 ,求数列
,求数列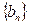 的前
的前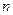 项和
项和查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
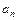 =1+
=1+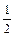 +
+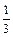 +…+
+…+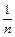 (n
(n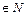 ),
),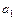 +
+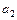 +…+
+…+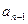 =g(n)(
=g(n)(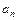 -1)的
-1)的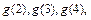 并猜想
并猜想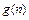 的表达式;
的表达式;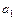 +
+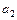 +…+
+…+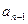 =g(n)(
=g(n)(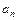 -1)对于大于1的一切自然数n都成立。
-1)对于大于1的一切自然数n都成立。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 中,
中, ,
, ,
, 证明:
证明: 是等比数列;
是等比数列; 的前
的前 项和为
项和为 ,求数列
,求数列 的通项公式,并求出n为何值时,
的通项公式,并求出n为何值时, 取得最小值,并说明理由。(参考数据:
取得最小值,并说明理由。(参考数据: )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com