
【题目】设函数f(x)=|ax-x2|+2b(a,b∈R).
(1)当b=0时,若不等式f(x)≤2x在x∈[0,2]上恒成立,求实数a的取值范围;
(2)已知a为常数,且函数f(x)在区间[0,2]上存在零点,求实数b的取值范围.
【答案】(1)[0,2];(2)见解析
【解析】试题分析:(1)不等式恒成立问题,一般利用变量分离转化为对应函数最值问题:![]() 恒成立,即
恒成立,即![]() ,即得实数a的取值范围;(2)先分离转化为对应函数交点问题:x|a-x|=-2b,根据a与[0,2]位置关系分类讨论,确定函数y=x|a-x|图像,再根据函数最大值与对称轴位置关系进行二级讨论,最终确定b的取值范围.
,即得实数a的取值范围;(2)先分离转化为对应函数交点问题:x|a-x|=-2b,根据a与[0,2]位置关系分类讨论,确定函数y=x|a-x|图像,再根据函数最大值与对称轴位置关系进行二级讨论,最终确定b的取值范围.
试题解析:(1)当b=0时,若不等式x|a-x|≤2x在x∈[0,2]上恒成立;
当x=0时,不等式恒成立,则a∈R;
当0<x≤2,则|a-x|≤2在(0,2]上恒成立,即-2≤x-a≤2在(0,2]上恒成立,
因为y=x-a在(0,2]上单调增,ymax=2-a,ymin>-a,则![]() ,解得:0≤a≤2;
,解得:0≤a≤2;
则实数a的取值范围为[0,2];
(2)函数f(x)在[0,2]上存在零点,即方程x|a-x|=-2b在[0,2]上有解;
设h(x)=![]()
当a≤0时,则h(x)=x2-ax,x∈[0,2],且h(x)在[0,2]上单调递增,所以h(x)min=h(0)=0,h(x)max=h(2)=4-2a,则当0≤-2b≤4-2a时,原方程有解,则a-2≤b≤0;
当a>0时,h(x)=![]() ,h(x)在
,h(x)在![]() 上单调增,在
上单调增,在![]() 上单调减,在[a,+∞)上单调增;
上单调减,在[a,+∞)上单调增;
①当![]() ≥2,即a≥4时,h(x)max=h(2)=2a-4,h(x)min=h(0)=0,
≥2,即a≥4时,h(x)max=h(2)=2a-4,h(x)min=h(0)=0,
则当0≤-2b≤2a-4时,原方程有解,则2-a≤b≤0;
②当![]() <2≤a,即2≤a<4时,h(x)max=h
<2≤a,即2≤a<4时,h(x)max=h![]() =
=![]() ,h(x)min=h(0)=0,则当0≤-2b≤
,h(x)min=h(0)=0,则当0≤-2b≤![]() 时,原方程有解,则-
时,原方程有解,则-![]() ≤b≤0;
≤b≤0;
③当0<a<2时,h(x)max=max![]() =max
=max![]() ,h(x)min=h(0)=0,
,h(x)min=h(0)=0,
当![]() ≥4-2a,即-4+4
≥4-2a,即-4+4![]() ≤a<2时,h(x)max=
≤a<2时,h(x)max=![]() ,则当0≤-2b≤
,则当0≤-2b≤![]() 时,原方程有解,则-
时,原方程有解,则-![]() ≤b≤0;
≤b≤0;
当![]() <4-2a,即0<a<-4+4
<4-2a,即0<a<-4+4![]() 时,h(x)max=4-2a,则当0≤-2b≤4-2a时,原方程有解,则a-2≤b≤0;
时,h(x)max=4-2a,则当0≤-2b≤4-2a时,原方程有解,则a-2≤b≤0;
综上,当a<-4+4![]() 时,实数b的取值范围为[a-2,0];
时,实数b的取值范围为[a-2,0];
当-4+4![]() ≤a<4时,实数b的取值范围为
≤a<4时,实数b的取值范围为![]() ;
;
当a≥4时,实数b的取值范围为![]() .
.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
在四棱锥P-ABCD中,BC∥AD,PA⊥PD,AD=2BC,AB=PB, E为PA的中点.
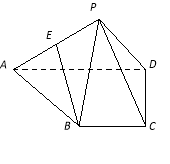
(1)求证:BE∥平面PCD;
(2)求证:平面PAB⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点
,点![]() 是圆
是圆![]()
![]() 上的任意一点,线段
上的任意一点,线段![]() 的垂直平分线与直线
的垂直平分线与直线![]() 交于点
交于点![]() .
.
(Ⅰ)求点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)若直线![]() 与点
与点![]() 的轨迹有两个不同的交点
的轨迹有两个不同的交点![]() 和
和![]() ,且原点
,且原点![]() 总在以
总在以![]() 为直径的圆的内部,求实数
为直径的圆的内部,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 短轴的左右两个端点分别为A,B,直线
短轴的左右两个端点分别为A,B,直线![]() 与x轴、y轴分别交于两点E,F,交椭圆于两点C,D.
与x轴、y轴分别交于两点E,F,交椭圆于两点C,D.
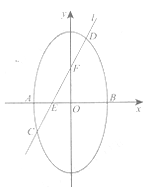
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设直线AD,CB的斜率分别为![]() ,若
,若![]() ,求k的值.
,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=si n![]() -2cos2
-2cos2![]() +1.
+1.
(1)求f(x)的最小正周期;
(2)若函数y=f(x)与y=g(x)的图象关于直线x=1对称,求当x∈![]() 时,y=g(x)的最大值.
时,y=g(x)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有外形相同的球分装三个盒子,每盒10个.其中,第一个盒子中7个球标有字母A、3个球标有字母B;第二个盒子中有红球和白球各5个;第三个盒子中则有红球8个,白球2个.试验按如下规则进行:先在第一号盒子中任取一球,若取得标有字母A的球,则在第二号盒子中任取一个球;若第一次取得标有字母B的球,则在第三号盒子中任取一个球.如果第二次取出的是红球,则称试验成功,那么试验成功的概率为( )
A.0.59 B.0.54 C.0.8 D.0.15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:对于任意
满足:对于任意![]() 且
且![]() 时,
时,![]() ,
,![]() .
.
(1)若![]() ,求证:
,求证:![]() 为等比数列;
为等比数列;
(2)若![]() .
.
① 求数列![]() 的通项公式;
的通项公式;
② 是否存在![]() ,使得
,使得![]() 为数列
为数列![]() 中的项?若存在,求出所有满足条件的
中的项?若存在,求出所有满足条件的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
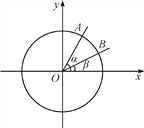
【题目】如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为![]() ,
,![]() .求:
.求:
(1)tan(α+β)的值;
(2)α+2β的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图.
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() .
.
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤.
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com