
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的方程为
的方程为![]() ,动圆
,动圆![]() 过点
过点![]() 和点
和点![]() .记两个圆的交点为
.记两个圆的交点为![]() 、
、![]() .
.
(1)如果直线![]() 的方程为
的方程为![]() ,求圆
,求圆![]() 的方程;
的方程;
(2)当动圆![]() 的面积最小时,求两个圆心距离
的面积最小时,求两个圆心距离![]() 的大小.
的大小.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)联立AB的方程和圆![]() 求得A和B的坐标,求出以点(3,0)和(1,0)为端点的弦的中垂线
求得A和B的坐标,求出以点(3,0)和(1,0)为端点的弦的中垂线![]() ,弦AB的中垂线方程为
,弦AB的中垂线方程为![]() ,联立解得
,联立解得![]() 的圆心坐标为(1,4),由此写出
的圆心坐标为(1,4),由此写出![]() 的方程;
的方程;
(2)当点(3,0)和点(1,0)为圆![]() 直径的两个端点时动圆
直径的两个端点时动圆![]() 的面积最小,求出
的面积最小,求出![]() 的坐标,利用两点间的距离公式求得两个圆心距离
的坐标,利用两点间的距离公式求得两个圆心距离![]() 的大小.
的大小.
解:(1)联立![]() ,
,
解得A和B的坐标分别为(1,0)和(3,2).
∵圆心在以(3,0)和(1,0)为端点的弦的中垂线上,
以点(3,0)和(1,0)为端点的弦的中垂线为![]() ,
,
弦AB的中垂线方程为![]() ,
,
联立解得![]() 的圆心坐标为(1,4),半径为
的圆心坐标为(1,4),半径为![]() ,
,
由此写出![]() 的方程为
的方程为![]() ;
;
(2)动圆![]() 的面积最小,则圆
的面积最小,则圆![]() 的圆心为点(3,0)和点(1,0)连线的中点.
的圆心为点(3,0)和点(1,0)连线的中点.
由中点坐标公式得![]() (1,0),又
(1,0),又![]() (2,1),
(2,1),![]() .
.


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
【题目】某书店销售刚刚上市的某高二数学单元测试卷,按事先拟定的价格进行5天试销,每种单价试销1天,得到如下数据:
单价x/元 | 18 | 19 | 20 | 21 | 22 |
销量y/册 | 61 | 56 | 50 | 48 | 45 |
(1)求试销![]() 天的销量的方差和
天的销量的方差和![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
附:  .
.
(2)预计以后的销售中,销量与单价服从上题中的回归直线方程,已知每册单元测试卷的成本是10元,为了获得最大利润,该单元测试卷的单价应定为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是不重合直线,
是不重合直线,![]() 是不重合平面,则下列命题
是不重合平面,则下列命题
①若![]() ,则
,则![]() ∥
∥![]()
②若![]() ∥
∥![]() ∥
∥![]() ,则
,则![]() ∥
∥![]()
③若![]() ∥
∥![]() 、
、![]() ∥
∥![]() ,则
,则![]() ∥
∥![]()
④若![]() ,则
,则![]() ∥
∥![]()
⑤若![]() ,则
,则![]() ∥
∥![]()
为假命题的是
A. ①②③ B. ①②⑤ C. ③④⑤ D. ①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级期末考试的学生中抽出 6![]() 名学生,其成绩(均为整数)的频率分布直方图如图所示.
名学生,其成绩(均为整数)的频率分布直方图如图所示.
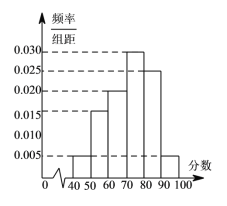
(1)估计这次考试的中位数
(2)假设分数在![]() 的学生的成绩都不相同,且都在
的学生的成绩都不相同,且都在![]() 分以上,现用简单随机抽样方法,从
分以上,现用简单随机抽样方法,从![]() 这
这 ![]() 个数中任取
个数中任取 ![]() 个数,求这
个数,求这 ![]() 个数恰好是两个学生的成绩的概率.
个数恰好是两个学生的成绩的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在![]() 处有一港口,两艘海轮
处有一港口,两艘海轮![]() 同时从港口
同时从港口![]() 处出发向正北方向匀速航行,海轮
处出发向正北方向匀速航行,海轮![]() 的航行速度为20海里/小时,海轮
的航行速度为20海里/小时,海轮![]() 的航行速度大于海轮
的航行速度大于海轮![]() .在港口
.在港口![]() 北偏东60°方向上的
北偏东60°方向上的![]() 处有一观测站,1小时后在
处有一观测站,1小时后在![]() 处测得与海轮
处测得与海轮![]() 的距离为30海里,且
的距离为30海里,且![]() 处对两艘海轮
处对两艘海轮![]() ,
,![]() 的视角为30°.
的视角为30°.

(1)求观测站![]() 到港口
到港口![]() 的距离;
的距离;
(2)求海轮![]() 的航行速度.
的航行速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com