
【题目】已知函数f(x)= ![]() +alnx﹣2,曲线y=f(x)在点P(1,f(1))处的切线与直线y=x+3垂直.
+alnx﹣2,曲线y=f(x)在点P(1,f(1))处的切线与直线y=x+3垂直.
(1)求实数a的值;
(2)记g(x)=f(x)+x﹣b(b∈R),若函数g(x)在区间[e﹣1 , e]上有两个零点,求实数b的取值范围;
(3)若不等式πf(x)>( ![]() )1+x﹣lnx在|t|≤2时恒成立,求实数x的取值范围.
)1+x﹣lnx在|t|≤2时恒成立,求实数x的取值范围.
【答案】
(1)解:函 数 f( x) 的 定 义 域 为 ( 0,+∞),f′( x)= ![]() .
.
∵曲线y=f(x)在点P(1,f(1))处的切线与直线y=x+3垂直,
∴f′( 1)=﹣2+a=﹣1,解 得 a=1.
(2)解:g( x)= ![]() +lnx+x﹣2﹣b( x>0),g′( x)=
+lnx+x﹣2﹣b( x>0),g′( x)= ![]() ,
,
由 g′( x)>0,得 x>1,由 g′( x)<0,得 0<x<1,
∴g( x) 的 单 调 递 增 区 间 是 ( 1,+∞),单 调 递 减 区 间 为 ( 0,1),
当 x=1 时,g( x) 取 得 极 小 值 g( 1),
∵函 数 g( x) 在 区 间[e﹣1,e]上 有 两 个 零 点,∴ 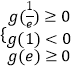
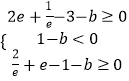 ,解得1
,解得1 ![]() ,
,
∴b 的 取 值 范 围 是 ( 1, ![]() +e﹣1];
+e﹣1];
(3)解:∵π f(x)>( ![]() )t+x﹣lnx 在|t|≤2 时 恒 成 立,∴f( x)>﹣t﹣x+lnx,
)t+x﹣lnx 在|t|≤2 时 恒 成 立,∴f( x)>﹣t﹣x+lnx,
即xt+x2﹣2x+2>0 在|t|≤2 时 恒 成 立,令 g( t)=xt+x2﹣2x+2,(x>0),
∴只 需 g(﹣2)>0,即 x2﹣4x+2>0
解 得x∈( 0,2﹣ ![]() )∪(2+
)∪(2+ ![]() ,+∞)
,+∞)
【解析】(1)根据导数的几何意义,得 f′( 1)=﹣1,解得a,(2)g( x)= ![]() +lnx+x﹣2﹣b( x>0),g′( x)=
+lnx+x﹣2﹣b( x>0),g′( x)= ![]() ,可得当 x=1 时,g( x) 取 得 极 小 值 g( 1);可得函 数 g( x) 在 区 间[e﹣1,e]上 有 两 个 零 点,
,可得当 x=1 时,g( x) 取 得 极 小 值 g( 1);可得函 数 g( x) 在 区 间[e﹣1,e]上 有 两 个 零 点, 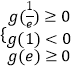
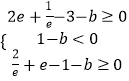 ,解得实数b的取值范围; (3)π f(x)>(
,解得实数b的取值范围; (3)π f(x)>( ![]() )t+x﹣lnx 在|t|≤2 时 恒 成 立,f( x)>﹣t﹣x+lnx,即t+x2﹣2x+2>0 在|t|≤2 时 恒 成 立,令 g( t)=xt+x2﹣2x+2,x>0,只 需 g(﹣2)>0,即可
)t+x﹣lnx 在|t|≤2 时 恒 成 立,f( x)>﹣t﹣x+lnx,即t+x2﹣2x+2>0 在|t|≤2 时 恒 成 立,令 g( t)=xt+x2﹣2x+2,x>0,只 需 g(﹣2)>0,即可
【考点精析】通过灵活运用函数的最大(小)值与导数,掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.
比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某市居民自来水收费标准如下:每户每月用水不超过4吨时,每吨为1.80元,当用水超过4吨时,超过部分每吨3.00元.某月甲、乙两户共交水费y元,已知甲、乙两用户该月用水量分别为5x,3x吨. (Ⅰ) 若x=1,求该月甲、乙两户的水费;
(Ⅱ) 求y关于x的函数;
(Ⅲ) 若甲、乙两户该月共交水费26.4元,分别求出甲、乙两户该月的用水量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,AF=![]() AD=a,G是EF的中点.
AD=a,G是EF的中点.
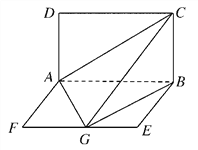
(1)求证:平面AGC⊥平面BGC;
(2)求GB与平面AGC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在二项式( ![]() +
+ ![]() )n展开式中,前三项的系数成等差数列. 求:(1)展开式中各项系数和;
)n展开式中,前三项的系数成等差数列. 求:(1)展开式中各项系数和;
【答案】解:由题意得2 ![]() ×
× ![]() =1+
=1+ ![]() ×
× ![]() ,
,
化为:n2﹣9n+8=0,解得n=1(舍去)或8.
∴n=8.
在 ![]() 中,令x=1,可得展开式中各项系数和=
中,令x=1,可得展开式中各项系数和= ![]() =
= ![]() .
.
(1)展开式中系数最大的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设复数z=2m+(4-m2)i,当实数m取何值时,复数z对应的点:
(1)位于虚轴上?
(2)位于一、三象限?
(3)位于以原点为圆心,以4为半径的圆上?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县农民年均收入服从μ=500元,σ=20元的正态分布,求:
(1)此县农民的年均收入在500~520元之间的人数的百分比;
(2)此县农民的年均收入超过540元的人数的百分比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD-A1B1C1D1中,如图.
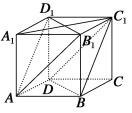
(1)求证:平面AB1D1∥平面C1BD;
(2)试找出体对角线A1C与平面AB1D1和平面C1BD的交点E,F,并证明:A1E=EF=FC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com