
分析 根据对数函数的图象和性质,可判断①;根据奇函数的性质,可判断②;根据映射的与定义,可判断③;根据指数函数的图象和性质,可判断④.
解答 解:对于①,当x=-1时,loga(2x-1)-1=-1恒成立,故函数f(x)=loga(2x-1)-1的图象过定点(1,-1),故①正确;
对于②,定义在R上的奇函数f(x),f(0)=-f(0)=0,故②正确;
对于③,A=R,B=R,$f:x→y=\frac{1}{x+1}$,则A中元素-1在B中没有对应的元素,故f不是A到B的映射,故③错误;
对于④,在同一坐标系中,y=2x与y=$(\frac{1}{2})^{2}$=2-x的图象关于y轴对称,故④正确.
故真命题的序号是:①②④,
故答案为:①②④.
点评 本题考查的知识点是命题的真假判断与应用,函数的图象和性质,难度中档.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 4 | C. | 4$\sqrt{2}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
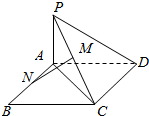 如图:ABCD为矩形,PA⊥平面ABCD,PA=AD=1,AB=2,M、N分别是PC、AB中点,请选择适当的坐标系证明:MN⊥平面PCD.
如图:ABCD为矩形,PA⊥平面ABCD,PA=AD=1,AB=2,M、N分别是PC、AB中点,请选择适当的坐标系证明:MN⊥平面PCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | (-∞,2] | C. | (-∞,-2)∪(-2,1] | D. | [1,2)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com