
【题目】如图,平面四边形ABCD中,AB= ![]() ,AD=2
,AD=2 ![]() ,CD=
,CD= ![]() ,∠CBD=30°,∠BCD=120°.
,∠CBD=30°,∠BCD=120°.
(1)求BD的长;
(2)求∠ADC的度数.
【答案】
(1)
解:方法一:在△BCD中,由正弦定理得:
![]() ,即
,即 ![]()
解得BD=3
方法二:由已知得∠BDC=30°,故 ![]()
由余弦定理得:
BD2=CD2+BC2﹣2CDBCcos∠BCD
= ![]()
∴BD=3
(2)
解:在△ABD中,由余弦定理得:
![]() )
)
∴∠ADB=45° …(8分)
由已知∠BDC=30°…(9分)
∴∠ADC=∠ADB+∠BDC=45°+30°=75°
【解析】(1)方法一:在△BCD中,由题意和正弦定理求出BD;方法二:由∠BDC=30°求出BC,利用条件和余弦定理列出方程,求出BD;(2)在△ABD中,利用条件和余弦定理求出cos∠ADB的值,结合图象求出∠ADC的度数.
【考点精析】通过灵活运用正弦定理的定义和余弦定理的定义,掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.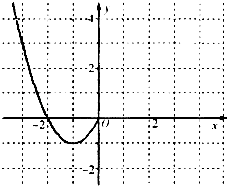
(1)现已画出函数f(x)在y轴左侧的图象,如图所示,请补出完整函数f(x)的图象,并根据图象写出函数f(x)的增区间;
(2)写出函数f(x)的解析式和值域;
(3)若方程f(x)﹣m=0有四个解,求m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,平面A1BC⊥侧面A1ABB1 , 且AA1=AB=2 
(1)求证:AB⊥BC;
(2)若AC=2 ![]() ,求锐二面角A﹣A1C﹣B的大小.
,求锐二面角A﹣A1C﹣B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,左、右焦点分别为F1 , F2 , 点G在椭圆C上,且
,左、右焦点分别为F1 , F2 , 点G在椭圆C上,且 ![]()
![]() =0,△GF1F2的面积为2.
=0,△GF1F2的面积为2. 
(1)求椭圆C的方程;
(2)直线l:y=k(x﹣1)(k<0)与椭圆Γ相交于A,B两点.点P(3,0),记直线PA,PB的斜率分别为k1 , k2 , 当 ![]() 最大时,求直线l的方程.
最大时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列A:a1 , a2 , …,an(n≥3)中ai∈N*(1≤i≤n)且对任意的2≤k≤n﹣1,ak+1+ak﹣1>2ak恒成立,则称数列A为“U﹣数列”.
(Ⅰ)若数列1,x,y,7为“U﹣数列”,写出所有可能的x,y;
(Ⅱ)若“U﹣数列”A:a1 , a2 , …,an中,a1=1,an=2017,求n的最大值;
(Ⅲ)设n0为给定的偶数,对所有可能的“U﹣数列”A:a1 , a2 , …,an0 , 记M=max{a1 , a2 , …,an0},其中max{x1 , x2 , …,xs}表示x1 , x2 , …,xs这s个数中最大的数,求M的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面使用类比推理正确的是( )
A.直线a∥b,b∥c,则a∥c,类推出:向量 ![]() ,
, ![]() ,则
,则 ![]()
B.同一平面内,直线a,b,c,若a⊥c,b⊥c,则a∥b.类推出:空间中,直线a,b,c,若a⊥c,b⊥c,则a∥b
C.实数a,b,若方程x2+ax+b=0有实数根,则a2≥4b.类推出:复数a,b,若方程x2+ax+b=0有实数根,则a2≥4b
D.以点(0,0)为圆心,r为半径的圆的方程为x2+y2=r2 . 类推出:以点(0,0,0)为球心,r为半径的球的方程为x2+y2+z2=r2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)求证f(x)是R上的单调增函数;
(2)求函数f(x)的值域;
(3)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)>0恒成立,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com