
【题目】某地级市共有200000中小学生,其中有7%学生在2017年享受了“国家精准扶贫”政策,在享受“国家精准扶贫”政策的学生中困难程度分为三个等次:一般困难、很困难、特别困难,且人数之比为5:3:2,为进一步帮助这些学生,当地市政府设立“专项教育基金”,对这三个等次的困难学生每年每人分别补助1000元、1500元、2000元。经济学家调查发现,当地人均可支配年收入较上一年每增加n%,一般困难的学生中有3n%会脱贫,脱贫后将不再享受“精准扶贫”政策,很困难的学生中有2n%转为一般困难,特别困难的学生中有n%转为很困难。现统计了该地级市2013年到2017年共5年的人均可支配年收入,对数据初步处理后得到了如图所示的散点图和表中统计量的值,其中年份![]() 取13时代表2013年,
取13时代表2013年, ![]() 与
与![]() (万元)近似满足关系式
(万元)近似满足关系式![]() ,其中
,其中![]() 为常数。(2013年至2019年该市中学生人数大致保持不变)
为常数。(2013年至2019年该市中学生人数大致保持不变)


其中![]() ,
, ![]()
(Ⅰ)估计该市2018年人均可支配年收入;
(Ⅱ)求该市2018年的“专项教育基金”的财政预算大约为多少?
附:①对于一组具有线性相关关系的数据![]() ,其回归直线方程
,其回归直线方程
![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
②
【答案】(Ⅰ)2.8(万);(Ⅱ)1624万.
【解析】试题分析:(Ⅰ)由![]() 得
得![]() ,所以
,所以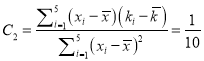 ,
, ![]() ,即可得解;
,即可得解;
(Ⅱ)由题意知2017年时该市享受“国家精准扶贫”政策的学生人数,一般困难、很困难、特别困难的中学生人数, 018年人均可支配收入比2017年增长![]() ,据此可得2018年该市特别困难、很困难、一般困难的学生的中学生人数,即可得解.
,据此可得2018年该市特别困难、很困难、一般困难的学生的中学生人数,即可得解.
试题解析:
(Ⅰ)因为![]() ,所以
,所以![]() .
.
由![]() 得
得![]() ,
,
所以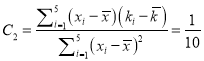 ,
, ![]() ,所以
,所以![]() ,所以
,所以![]() .
.
当![]() 时,2018年人均可支配年收入
时,2018年人均可支配年收入![]() (万)
(万)
(Ⅱ)由题意知2017年时该市享受“国家精准扶贫”政策的学生共200000×7%=14000人
一般困难、很困难、特别困难的中学生依次有7000人、4200人、2800人, 2018年人均可支配收入比2017年增长![]()
所以2018年该市特别困难的中学生有2800×(1-10%)=2520人,
很困难的学生有4200×(1-20%)+2800×10%=3640人
一般困难的学生有7000×(1-30%)+4200×20%=5740人.
所以2018年的“专项教育基金”的财政预算大约为5740×1000+3640×1500+2520×2000=1624万


科目:高中数学 来源: 题型:
【题目】选修4 — 4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为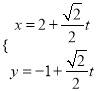 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ).
).
(1)分别写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的两个焦点分别为
的两个焦点分别为![]() ,点M(1,0)与椭圆短轴的两个端点的连线相互垂直.
,点M(1,0)与椭圆短轴的两个端点的连线相互垂直.
(1)求椭圆C的方程;
(2)过点M(1,0)的直线与椭圆C相交于A、B两点,设点N(3,2),记直线AN、BN的斜率分别为k1、k2,求证:k1+k2为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域在![]() 上的函数
上的函数![]() 满足对于任意的
满足对于任意的![]() ,都有
,都有![]() ,当且仅当
,当且仅当![]() 时,
时,![]() 成立.
成立.
(1)设![]() ,求证
,求证![]() ;
;
(2)设![]() ,若
,若![]() ,试比较x1与x2的大小;
,试比较x1与x2的大小;
(3)若![]() ,解关于x的不等式
,解关于x的不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知随机变量ξi满足P(ξi=1)=pi,P(ξi=0)=1-pi,i=1,2.若0<p1<p2<![]() ,则( )
,则( )
A. E(ξ1)<E(ξ2),D(ξ1)<D(ξ2)
B. E(ξ1)<E(ξ2),D(ξ1)>D(ξ2)
C. E(ξ1)>E(ξ2),D(ξ1)<D(ξ2)
D. E(ξ1)>E(ξ2),D(ξ1)>D(ξ2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年10月1日为庆祝中国人民共和国成立70周年在北京天安门广场举行了盛大的阅兵仪式,共有580台(套)装备、160余架各型飞机接受检阅,受阅装备均为中国国产现役主战装备,其中包括部分首次公开亮相的新型装备.例如,在无人作战第三方队中就包括了两型侦察干扰无人机,可以在遥控设备或自备程序控制操纵的情况下执行任务,进行对敌方通讯设施的电磁压制和干扰,甚至压制敌人的防空系统.某作战部门对某处的战场实施“电磁干扰”实验,据测定,该处的“干扰指数”与无人机干扰源的强度和距离之比成正比,比例系数为常数![]() (
(![]() ),现已知相距36
),现已知相距36![]() 的
的![]() 、
、![]() 两处配置两架无人机干扰源,其对敌干扰的强度分别为1和
两处配置两架无人机干扰源,其对敌干扰的强度分别为1和![]() (
(![]() ),它们连线段上任意一点
),它们连线段上任意一点![]() 处的干扰指数
处的干扰指数![]() 等于两机对该处的干扰指数之和,设
等于两机对该处的干扰指数之和,设![]() (
(![]() ).
).
(1)试将![]() 表示为
表示为![]() 的函数,指出其定义域;
的函数,指出其定义域;
(2)当![]() ,
,![]() 时,试确定“干扰指数”最小时
时,试确定“干扰指数”最小时![]() 所处位置.
所处位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设随机变量ξ服从正态分布N(0,1),则下列结论正确的是( )
①P(|ξ|<a)=P(ξ<a)+P(ξ>-a)(a>0);②P(|ξ|<a)=2P(ξ<a)-1(a>0);③P(|ξ|<a)=1-2P(ξ<a)(a>0);④P(|ξ|<a)=1-P(|ξ|≥a)(a>0).
A. ①② B. ②③
C. ①④ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人同时参加一次数学测试,共有20道选择题,每题均有4个选项,答对得3分,答错或不答得0分,甲和乙都解答了所有的试题,经比较,他们只有2道题的选项不同,如果甲最终的得分为54分,那么乙的所有可能的得分值组成的集合为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com