
ЁОЬтФПЁПдкКтбєЪаЁАДДШЋЙњЮФУїГЧЪаЁБЃЈМђГЦЁАДДЮФЁБЃЉЛюЖЏжаЃЌЪаНЬг§ОжЖдБОЪаAЃЌBЃЌCЃЌDЫФЫљИпжабЇаЃАДИїаЃШЫЪ§ЗжВуГщбљЃЌЫцЛњГщВщСЫ200ШЫЃЌНЋЕїВщЧщПіНјааећРэКѓжЦГЩЯТБэЃК
бЇаЃ | A | B | C | D |
ГщВщШЫЪ§ | 10 | 15 | 100 | 75 |
ЁАДДЮФЁБЛюЖЏжаВЮгыЕФШЫЪ§ | 9 | 10 | 80 | 49 |
МйЩшУПУћИпжабЇЩњЪЧЗёВЮгыЁАДДЮФЁБЛюЖЏЪЧЯрЛЅЖРСЂЕФ
ЃЈ1ЃЉШєБОЪаЙВ8000УћИпжабЇЩњЃЌЙРМЦCбЇаЃВЮгыЁАДДЮФЁБЛюЖЏЕФШЫЪ§ЃЛ
ЃЈ2ЃЉдкЩЯБэжаДгAЃЌBСНаЃУЛгаВЮгыЁАДДЮФЁБЛюЖЏЕФЭЌбЇжаЫцЛњГщШЁ2ШЫЃЌЧѓЧЁКУAЃЌBСНаЃИїга1ШЫУЛгаВЮгыЁАДДЮФЁБЛюЖЏЕФИХТЪЃЛ
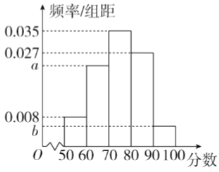
ЃЈ3ЃЉдкЫцЛњГщВщЕФ200УћИпжабЇЩњжаЃЌНјааЮФУїЫибјзлКЯЫижЪВтЦРЃЈТњЗжЮЊ100ЗжЃЉЃЌЕУЕНШчЩЯЕФЦЕТЪЗжВМжБЗНЭМЃЌЦфжа![]() ЃЎЧѓaЃЌbЕФжЕЃЌВЂЙРМЦВЮгыВтЦРЕФбЇЩњЕУЗжЕФжаЮЛЪ§ЃЎЃЈМЦЫуНсЙћБЃСєСНЮЛаЁЪ§ЃЉЃЎ
ЃЎЧѓaЃЌbЕФжЕЃЌВЂЙРМЦВЮгыВтЦРЕФбЇЩњЕУЗжЕФжаЮЛЪ§ЃЎЃЈМЦЫуНсЙћБЃСєСНЮЛаЁЪ§ЃЉЃЎ
ЁОД№АИЁПЃЈ1ЃЉ3200ЃЈ2ЃЉ![]() ЃЈ3ЃЉжаЮЛЪ§ЮЊ
ЃЈ3ЃЉжаЮЛЪ§ЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЧѓЕУCбЇаЃИпжаЩњЕФзмШЫЪ§ЃЌдйГЫвдCбЇаЃЫљеМЕФБШР§![]() ЃЌМШЕУД№АИЃЛ
ЃЌМШЕУД№АИЃЛ
ЃЈ2ЃЉЗжБ№БъМЧAЃЌBСНаЃУЛгаВЮгыЁАДДГЧЁБЛюЖЏЭЌбЇЃЌаДГіШЮШЁСНШЫЕФЫљгаЛљБОЪТМўЃЌбЁГіЦфжаТњзуЕФЬѕМўЕФЛљБОЪТМўЃЌгЩЙХЕфИХаЭЧѓИХТЪЕФЙЋЪНЃЌЧѓЕУД№АИЃЛ
ЃЈ3ЃЉгЩЦЕТЪЗжВМжБЗНЭМЕФУцЛ§ЮЊ1ЙЙНЈЗНГЬЃЌСЊЯЕвбжЊЧѓЕУ![]() ЃЌгЩЧАСНзщЕФЦЕТЪКЭаЁгк0.5ЃЌЧАШ§зщЕФЦЕТЪКЭДѓгк0.5ЃЌЫљвджаЮЛЪ§дкЕкШ§зщЃЌЧвдкЕкШ§зщжаЕФЦЕТЪЧЁеМ0.18ЃЌЧѓГіЕкШ§зщЕФГЄЖШМгЩЯ70ЃЌМШЕУД№АИ.
ЃЌгЩЧАСНзщЕФЦЕТЪКЭаЁгк0.5ЃЌЧАШ§зщЕФЦЕТЪКЭДѓгк0.5ЃЌЫљвджаЮЛЪ§дкЕкШ§зщЃЌЧвдкЕкШ§зщжаЕФЦЕТЪЧЁеМ0.18ЃЌЧѓГіЕкШ§зщЕФГЄЖШМгЩЯ70ЃЌМШЕУД№АИ.
ЃЈ1ЃЉCбЇаЃИпжаЩњЕФзмШЫЪ§ЮЊ![]() ЃЌ
ЃЌ
CбЇаЃВЮгыЁАДДЮФЁБЛюЖЏЕФШЫЪ§ЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉAаЃУЛгаВЮгыЁАДДГЧЁБЛюЖЏЕФет1ШЫМЧЮЊ![]() ЃЌBаЃУЛгаВЮгыЁАДДЮФЁБЛюЖЏЕФет5ШЫЗжБ№МЧЮЊ
ЃЌBаЃУЛгаВЮгыЁАДДЮФЁБЛюЖЏЕФет5ШЫЗжБ№МЧЮЊ![]()
![]()
![]()
![]()
![]() ЃЌ
ЃЌ
ШЮШЁ2ШЫЙВ15жжЧщПіЃЌШчЯТЃК![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ЃЌет15жжЧщПіЗЂЩњЕФПЩФмадЪЧЯрЕШЕФЃЎ
ЃЌет15жжЧщПіЗЂЩњЕФПЩФмадЪЧЯрЕШЕФЃЎ
ЩшЪТМўNЮЊГщШЁ2ШЫжаAЃЌBСНаЃИїга1ШЫУЛгаВЮгыЁАДДЮФЁБЛюЖЏЃЌга![]()
![]()
![]()
![]()
![]() ЃЌЙВ5жжЧщПіЃЎ
ЃЌЙВ5жжЧщПіЃЎ
дђ![]() ЃЎЙЪЧЁКУAЃЌBСНаЃИїга1ШЫУЛгаВЮгыЁАДДЮФЁБЛюЖЏЕФИХТЪЮЊ
ЃЎЙЪЧЁКУAЃЌBСНаЃИїга1ШЫУЛгаВЮгыЁАДДЮФЁБЛюЖЏЕФИХТЪЮЊ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉвРЬтвтЃЌ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЎ
ЃЎ
гж![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
вђЮЊ![]() ЃЌЫљвджаЮЛЪ§дкЕкШ§зщЃЌ
ЃЌЫљвджаЮЛЪ§дкЕкШ§зщЃЌ
ЫљвджаЮЛЪ§ЮЊ![]() ЃЎ
ЃЎ


 ЦпВЪЬтПЈПкЫугІгУвЛЕуЭЈЯЕСаД№АИ
ЦпВЪЬтПЈПкЫугІгУвЛЕуЭЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈ1ЃЉЬжТл![]() ЕФЕЅЕїадЃЛ
ЕФЕЅЕїадЃЛ
ЃЈ2ЃЉШчЙћЗНГЬ![]() гаСНИіВЛЯрЕШЕФНт
гаСНИіВЛЯрЕШЕФНт![]() ЃЌЧв
ЃЌЧв![]() ЃЌжЄУїЃК
ЃЌжЄУїЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() =
=![]() ЪЧОиеѓM=
ЪЧОиеѓM=![]() ЪєгкЬиеїжЕІЫ1=2ЕФвЛИіЬиеїЯђСПЃЎ
ЪєгкЬиеїжЕІЫ1=2ЕФвЛИіЬиеїЯђСПЃЎ
ЃЈЂёЃЉЧѓОиеѓMЃЛ
ЃЈЂђЃЉШє![]() ЃЌЧѓM10aЃЎ
ЃЌЧѓM10aЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАЫбЫїжИЪ§ЁБЪЧЭјУёЭЈЙ§ЫбЫїв§ЧцЃЌвдУПЬьЫбЫїЙиМќДЪЕФДЮЪ§ЮЊЛљДЁЫљЕУЕНЕФЭГМЦжИБъ.ЁАЫбЫїжИЪ§ЁБдНДѓЃЌБэЪОЭјУёЖдИУЙиМќДЪЕФЫбЫїДЮЪ§дНЖрЃЌЖдИУЙиМќДЪЯрЙиЕФаХЯЂЙизЂЖШвВдНИп.ЯТЭМЪЧ2017Фъ9дТЕН2018Фъ2дТетАыФъжаЃЌФГИіЙиМќДЪЕФЫбЫїжИЪ§БфЛЏЕФзпЪЦЭМ.

ИљОнИУзпЪЦЭМЃЌЯТСаНсТле§ШЗЕФЪЧЃЈ ЃЉ
A. етАыФъжаЃЌЭјУёЖдИУЙиМќДЪЯрЙиЕФаХЯЂЙизЂЖШГЪжмЦкадБфЛЏ
B. етАыФъжаЃЌЭјУёЖдИУЙиМќДЪЯрЙиЕФаХЯЂЙизЂЖШВЛЖЯМѕШѕ
C. ДгЭјУёЖдИУЙиМќДЪЕФЫбЫїжИЪ§РДПДЃЌШЅФъ10дТЗнЕФЗНВюаЁгк11дТЗнЕФЗНВю
D. ДгЭјУёЖдИУЙиМќДЪЕФЫбЫїжИЪ§РДПДЃЌШЅФъ12дТЗнЕФЦНОљжЕДѓгкНёФъ1дТЗнЕФЦНОљжЕ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪЕЪ§![]() ЃЌ
ЃЌ![]() ЪЧКЏЪ§
ЪЧКЏЪ§![]() ЕФСНИіСуЕу.
ЕФСНИіСуЕу.
ЃЈ1ЃЉЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉжЄУїЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкКтбєЪаЁАДДШЋЙњЮФУїГЧЪаЁБЃЈМђГЦЁАДДЮФЁБЃЉЛюЖЏжаЃЌЪаНЬг§ОжЖдБОЪаAЃЌBЃЌCЃЌDЫФЫљИпжабЇаЃАДИїаЃШЫЪ§ЗжВуГщбљЃЌЫцЛњГщВщСЫ200ШЫЃЌНЋЕїВщЧщПіНјааећРэКѓжЦГЩЯТБэЃК
бЇаЃ | A | B | C | D |
ГщВщШЫЪ§ | 10 | 15 | 100 | 75 |
ЁАДДЮФЁБЛюЖЏжаВЮгыЕФШЫЪ§ | 9 | 10 | 80 | 49 |

МйЩшУПУћИпжабЇЩњЪЧЗёВЮгыЁАДДЮФЁБЛюЖЏЪЧЯрЛЅЖРСЂЕФ
ЃЈ1ЃЉШєБОЪаЙВ8000УћИпжабЇЩњЃЌЙРМЦCбЇаЃВЮгыЁАДДЮФЁБЛюЖЏЕФШЫЪ§ЃЛ
ЃЈ2ЃЉдкЩЯБэжаДгAЃЌBСНаЃУЛгаВЮгыЁАДДЮФЁБЛюЖЏЕФЭЌбЇжаЫцЛњГщШЁ2ШЫЃЌЧѓЧЁКУAЃЌBСНаЃИїга1ШЫУЛгаВЮгыЁАДДЮФЁБЛюЖЏЕФИХТЪЃЛ
ЃЈ3ЃЉдкЫцЛњГщВщЕФ200УћИпжабЇЩњжаЃЌНјааЮФУїЫибјзлКЯЫижЪВтЦРЃЈТњЗжЮЊ100ЗжЃЉЃЌЕУЕНШчЩЯЕФЦЕТЪЗжВМжБЗНЭМЃЌЦфжа![]() ЃЎЧѓaЃЌbЕФжЕЃЌВЂЙРМЦВЮгыВтЦРЕФбЇЩњЕУЗжЕФжаЮЛЪ§ЃЎЃЈМЦЫуНсЙћБЃСєСНЮЛаЁЪ§ЃЉЃЎ
ЃЎЧѓaЃЌbЕФжЕЃЌВЂЙРМЦВЮгыВтЦРЕФбЇЩњЕУЗжЕФжаЮЛЪ§ЃЎЃЈМЦЫуНсЙћБЃСєСНЮЛаЁЪ§ЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ![]() x3+ax2+bxЃЌЧвfЁфЃЈЉ1ЃЉЃН0ЃЎ
x3+ax2+bxЃЌЧвfЁфЃЈЉ1ЃЉЃН0ЃЎ
ЃЈ1ЃЉЪдгУКЌaЕФДњЪ§ЪНБэЪОbЃЛ
ЃЈ2ЃЉЧѓfЃЈxЃЉЕФЕЅЕїЧјМфЃЛ
ЃЈ3ЃЉСюaЃНЉ1ЃЌЩшКЏЪ§fЃЈxЃЉдкx1ЁЂx2ЃЈx1ЃМx2ЃЉДІШЁЕУМЋжЕЃЌМЧЕуMЃЈx1ЃЌfЃЈx1ЃЉЃЉЃЌNЃЈx2ЃЌfЃЈx2ЃЉЃЉЃЎжЄУїЃКЯпЖЮMNгыЧњЯпfЃЈxЃЉДцдквьгкMЃЌNЕФЙЋЙВЕуЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгавЛИіГЄЗНаЮФОПщЃЌШ§ИіВрУцЛ§ЗжБ№ЮЊ8ЃЌ12ЃЌ24ЃЌЯжНЋЦфЯїГЩвЛИіе§ЫФУцЬхФЃаЭЃЌдђИУе§ЫФУцЬхФЃаЭРтГЄЕФзюДѓжЕЮЊЃЈ ЃЉ
A.2B.![]() C.4D.
C.4D.![]()
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com