
【题目】已知抛物线![]() 和点
和点![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于不同两点
交于不同两点![]() ,
,![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于另一点
交于另一点![]() .给出以下判断:
.给出以下判断:
①直线![]() 与直线
与直线![]() 的斜率乘积为
的斜率乘积为![]() ;
;
②![]() 轴;
轴;
③以![]() 为直径的圆与抛物线准线相切.
为直径的圆与抛物线准线相切.
其中,所有正确判断的序号是( )
A.①②③B.①②C.①③D.②③
【答案】B
【解析】
由题意,可设直线![]() 的方程为
的方程为![]() ,利用韦达定理判断第一个结论;将
,利用韦达定理判断第一个结论;将![]() 代入抛物线
代入抛物线![]() 的方程可得,
的方程可得,![]() ,从而,
,从而,![]() ,进而判断第二个结论;设
,进而判断第二个结论;设![]() 为抛物线
为抛物线![]() 的焦点,以线段
的焦点,以线段![]() 为直径的圆为
为直径的圆为![]() ,则圆心
,则圆心![]() 为线段
为线段![]() 的中点.设
的中点.设![]() ,
,![]() 到准线的距离分别为
到准线的距离分别为![]() ,
,![]() ,
,![]() 的半径为
的半径为![]() ,点
,点![]() 到准线的距离为
到准线的距离为![]() ,显然
,显然![]() ,
,![]() ,
,![]() 三点不共线,进而判断第三个结论.
三点不共线,进而判断第三个结论.
解:由题意,可设直线![]() 的方程为
的方程为![]() ,
,
代入抛物线![]() 的方程,有
的方程,有![]() .
.
设点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,
则![]() ,
,![]() .
.
所![]() .
.
则直线![]() 与直线
与直线![]() 的斜率乘积为
的斜率乘积为![]() .所以①正确.
.所以①正确.
将![]() 代入抛物线
代入抛物线![]() 的方程可得,
的方程可得,![]() ,从而,
,从而,![]() ,
,
根据抛物线的对称性可知,![]() ,
,![]() 两点关于
两点关于![]() 轴对称,
轴对称,
所以直线![]() 轴.所以②正确.
轴.所以②正确.
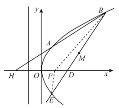
如图,设![]() 为抛物线
为抛物线![]() 的焦点,以线段
的焦点,以线段![]() 为直径的圆为
为直径的圆为![]() ,
,
则圆心![]() 为线段
为线段![]() 的中点.设
的中点.设![]() ,
,![]() 到准线的距离分别为
到准线的距离分别为![]() ,
,![]() ,
,![]() 的半径为
的半径为![]() ,点
,点![]() 到准线的距离为
到准线的距离为![]() ,显然
,显然![]() ,
,![]() ,
,![]() 三点不共线,
三点不共线,
则![]() .所以③不正确.
.所以③不正确.
故选:B.


科目:高中数学 来源: 题型:
【题目】已知甲箱中装有3个红球,2个黑球,乙箱中装有2个红球,3个黑球,这些球除颜色外完全相同,某商场举行有奖促销活动,规定顾客购物1000元以上,可以参与抽奖一次,设奖规则如下:每次分别从以上两个箱子中各随机摸出2个球,共4个球,若摸出4个球都是红球,则获得一等奖,奖金300元;摸出的球中有3个红球,则获得二等奖,奖金200元;摸出的球中有2个红球,则获得三等奖,奖金100元;其他情况不获奖,每次摸球结束后将球放回原箱中.
(1)求在1次摸奖中,获得二等奖的概率;
(2)若3人各参与摸奖1次,求获奖人数X的数学期望![]() ;
;
(3)若商场同时还举行打9折促销活动,顾客只能在两项促销活动中任选一项参与.假若你购买了价值1200元的商品,那么你选择参与哪一项活动对你有利?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若S![]() 是公差不为0的等差数列
是公差不为0的等差数列![]() 的前
的前![]() 项和,且
项和,且![]() 成等比数列。
成等比数列。
(1)求等比数列![]() 的公比;
的公比;
(2)若![]() ,求
,求![]() 的通项公式;
的通项公式;
(3)设![]() ,
, ![]() 是数列
是数列![]() 的前
的前![]() 项和,求使得
项和,求使得![]() 对所有
对所有![]() 都成立的最小正整数
都成立的最小正整数![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】实验中学从高二级部中选拔一个班级代表学校参加“学习强国知识大赛”,经过层层选拔,甲、乙两个班级进入最后决赛,规定回答1个相关问题做最后的评判选择由哪个班级代表学校参加大赛.每个班级6名选手,现从每个班级6名选手中随机抽取3人回答这个问题已知这6人中,甲班级有4人可以正确回答这道题目,而乙班级6人中能正确回答这道题目的概率每人均为![]() ,甲、乙两班级每个人对问题的回答都是相互独立,互不影响的.
,甲、乙两班级每个人对问题的回答都是相互独立,互不影响的.
(1)求甲、乙两个班级抽取的6人都能正确回答的概率;
(2)分别求甲、乙两个班级能正确回答题目人数的期望![]() 和方差
和方差![]() 、
、![]() ,并由此分析由哪个班级代表学校参加大赛更好?
,并由此分析由哪个班级代表学校参加大赛更好?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让税收政策更好的为社会发展服务,国家在修订《中华人民共和国个人所得税法》之后,发布了《个人所得税专项附加扣除暂行办法》,明确“专项附加扣除”就是子女教育、继续教育大病医疗、住房贷款利息、住房租金赠养老人等费用,并公布了相应的定额扣除标准,决定自2019年1月1日起施行,某机关为了调查内部职员对新个税方案的满意程度与年龄的关系,通过问卷调查,整理数据得如下2×2列联表:
40岁及以下 | 40岁以上 | 合计 | |
基本满意 | 15 | 30 | 45 |
很满意 | 25 | 10 | 35 |
合计 | 40 | 40 | 80 |
(1)根据列联表,能否有99%的把握认为满意程度与年龄有关?
(2)为了帮助年龄在40岁以下的未购房的8名员工解决实际困难,该企业拟员工贡献积分![]() (单位:分)给予相应的住房补贴
(单位:分)给予相应的住房补贴![]() (单位:元),现有两种补贴方案,方案甲:
(单位:元),现有两种补贴方案,方案甲:![]() ;方案乙:
;方案乙: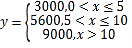 .已知这8名员工的贡献积分为2分,3分,6分,7分,7分,11分,12分,12分,将采用方案甲比采用方案乙获得更多补贴的员工记为“
.已知这8名员工的贡献积分为2分,3分,6分,7分,7分,11分,12分,12分,将采用方案甲比采用方案乙获得更多补贴的员工记为“![]() 类员工”.为了解员工对补贴方案的认可度,现从这8名员工中随机抽取4名进行面谈,求恰好抽到3名“
类员工”.为了解员工对补贴方案的认可度,现从这8名员工中随机抽取4名进行面谈,求恰好抽到3名“![]() 类员工”的概率。
类员工”的概率。
附:![]() ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,动点
中,动点![]() 与两定点
与两定点![]() ,
,![]() 连线的斜率之积为
连线的斜率之积为![]() ,记点
,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知点![]() ,过原点
,过原点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点(点
两点(点![]() 在第一象限),求四边形
在第一象限),求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家文明城市评审委员会对甲、乙两个城市是否能入围“国家文明城市”进行走访调查,派出10人的调查组,先后到甲、乙两个城市的街道、社区进行问卷调查,然后打分(满分100分),他们给出甲、乙两个城市分数的茎叶图如图所示:
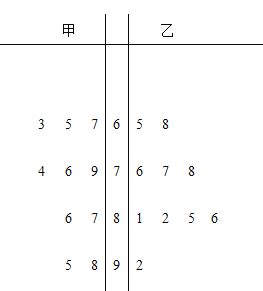
(1)请你用统计学的知识分析哪个城市更应该入围“国家文明城市”,并说明理由;
(2)从甲、乙两个城市的打分中各抽取2个,在已知有大于80分的条件下,求抽到乙城市的分数都小于80分的概率.
(参考数据:![]() ,
,![]()
![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com