
分析 (1)设Q(x0,2),代入抛物线方程,结合抛物线的定义,可得p=2,进而得到抛物线方程;
(2)设M(x1,y1),N(x2,y2),求出MN的中点T的坐标,利用垂直平分,建立方程,即可得出M,N,使得M,N关于直线l对称.
解答 解:(1)设Q(x0,2),P(0,2)代入由y2=2px(p>0)中得x0=$\frac{2}{p}$,
所以|PQ|=$\frac{2}{p}$,|QF|=$\frac{p}{2}$+$\frac{2}{p}$,
由题设得$\frac{p}{2}$+$\frac{2}{p}$=2×$\frac{2}{p}$,解得p=-2(舍去)或p=2.
所以C的方程为y2=4x.
(2)设M(x1,y1),N(x2,y2),则kMN=$\frac{4}{{y}_{1}+{y}_{2}}$,
MN的中点T的坐标为($\frac{{{y}_{1}}^{2}+{{y}_{2}}^{2}}{8}$,$\frac{{y}_{1}+{y}_{2}}{2}$),
∵M,N关于直线l对称,∴MN⊥l,∴$\frac{4}{{y}_{1}+{y}_{2}}$=1①,
∵中点T在直线l上,∴$\frac{{{y}_{1}}^{2}+{{y}_{2}}^{2}}{8}$+$\frac{{y}_{1}+{y}_{2}}{2}$-4=0②,
由①②可得y1+y2=4,y1y2=0,
∴y1=0,y2=4,
∴C上存在两点(0,0),(4,4),使得M,N关于直线l对称.
点评 本题考查抛物线的方程,考查直线与抛物线的位置关系,考查韦达定理的运用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2楼 | B. | 3楼 | C. | 4楼 | D. | 8楼 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
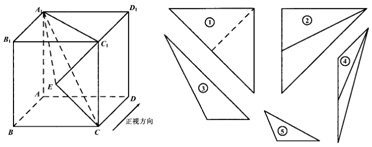
| A. | ①和⑤ | B. | ②和③ | C. | ④和⑤ | D. | ④和③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | -$\frac{1}{6}$ | C. | $\frac{1}{6}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 排队人数 | 0 | 1 | 2 | 3 | 4 | 5人以上 |
| 概率 | 0.1 | 0.16 | 0.3 | 0.3 | 0.1 | 0.04 |
| A. | 0.56 | B. | 0.44 | C. | 0.26 | D. | 0.14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 9 | C. | 8 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com