
【题目】已知函数![]() ,其中
,其中![]() ;
;
(l)判断函数![]() 是否存在极值,若存在,请判断是极大值还是极小值;若不存在,说明理由;
是否存在极值,若存在,请判断是极大值还是极小值;若不存在,说明理由;
(2)讨论在![]() 上函数
上函数![]() 的零点个数.
的零点个数.
【答案】(1)见解析;(2)见解析
【解析】
(1) ![]() ,设
,设![]() ,
,![]() ,因此
,因此![]() 单调递减,
单调递减,![]() ,讨论
,讨论![]() 正负即可判断出极值情况;
正负即可判断出极值情况;
(2)由(1)可知若![]() 时,
时,![]() 恒为增函数,计算可知
恒为增函数,计算可知![]() ,此时无零点, 若
,此时无零点, 若![]() 时,
时, ![]() ,可求得
,可求得![]() ,讨论
,讨论![]() 与
与![]() 的关系,及若
的关系,及若![]() ,
,![]() ,函数在区间
,函数在区间![]() 的单调性及函数值在区间端点的符号,即可得出结论.
的单调性及函数值在区间端点的符号,即可得出结论.
(1)![]() ,设
,设![]() ,
,
![]() ,因此
,因此![]() 单调递减,
单调递减,
![]() ,
,
又![]() 时,
时,![]() ,
,
若![]() ,即
,即![]() 时,
时,
![]() ,使
,使![]() ;
;
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
![]() 在
在![]() 处取极大值,不存在极小值.
处取极大值,不存在极小值.
若![]() ,即
,即![]() ,
,![]() ,
,
![]() 在
在![]() 单调递增,此时
单调递增,此时![]() 无极值.
无极值.
(2)由第一问结论可知:
(i)若![]() 时,由上问可知:
时,由上问可知:
![]() ,
,
即![]() 时函数没有零点.
时函数没有零点.
(ii)若![]() 时,
时,![]() 时
时![]() 单调递增;
单调递增;
![]() 时,
时,![]() 单调递减.
单调递减.
由![]() ,得
,得![]() ,
,
从而![]() ,再设
,再设![]() ,
,
则![]() ,从而a关于
,从而a关于![]() 单调递增.
单调递增.
①若![]() ,此时
,此时![]() ,
,
若![]() 得
得![]() 或
或![]() ,
,
所以![]() 时无零点;
时无零点;
若![]() 得
得![]() ,
,
所以![]() 时有一个零点;
时有一个零点;
当![]() ,
,![]() ,有一个零点.
,有一个零点.
因此![]() 时无零点;
时无零点;
![]() 时有一个零点;
时有一个零点;
②![]() 此时
此时![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,
设![]() ,
,
则![]() ,
,
所以![]() ,
,
若![]() 即
即![]() ,即
,即![]() 时无零点;
时无零点;
若![]() 即
即![]() ,即
,即![]() 时有一个零点.
时有一个零点.
综上所述:![]() 时无零点;
时无零点;
![]() 时有一个零点.
时有一个零点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
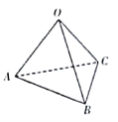
【题目】发展“会员”、提供优惠,成为不少实体店在网购冲击下吸引客流的重要方式.某连锁店为了吸引会员,在2019年春节期间推出一系列优惠促销活动.抽奖返现便是针对“白金卡会员”、“金卡会员”、“银卡会员”、“基本会员”不同级别的会员享受不同的优惠的一项活动:“白金卡会员”、“金卡会员”、“银卡会员”、“基本会员”分别有4次、3次、2次、1次抽奖机会.抽奖机如图:抽奖者第一次按下抽奖键,在正四面体的顶点![]() 出现一个小球,再次按下抽奖键,小球以相等的可能移向邻近的顶点之一,再次按下抽奖键,小球又以相等的可能移向邻近的顶点之一……每一个顶点上均有一个发光器,小球在某点时,该点等可能发红光或蓝光,若出现红光则获得2个单位现金,若出现蓝光则获得3个单位现金.
出现一个小球,再次按下抽奖键,小球以相等的可能移向邻近的顶点之一,再次按下抽奖键,小球又以相等的可能移向邻近的顶点之一……每一个顶点上均有一个发光器,小球在某点时,该点等可能发红光或蓝光,若出现红光则获得2个单位现金,若出现蓝光则获得3个单位现金.
(1)求“银卡会员”获得奖金的分布列;
(2)![]() 表示第
表示第![]() 次按下抽奖键,小球出现在
次按下抽奖键,小球出现在![]() 点处的概率.
点处的概率.
①求![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
②写出![]() 与
与![]() 关系式,并说明理由.
关系式,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以直角坐标系的原点
为参数).以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立坐标系,曲线
轴的正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 满足
满足![]() ,
,![]() ,记数列
,记数列![]() 的前n项和是
的前n项和是![]() ,则( )
,则( )
A.若数列![]() 是常数列,则
是常数列,则![]()
B.若![]() ,则数列
,则数列![]() 单调递减
单调递减
C.若![]() ,则
,则![]()
D.若![]() ,任取
,任取![]() 中的9项
中的9项![]() 构成数列
构成数列![]() 的子数列
的子数列![]() ,则
,则![]() 不全是单调数列
不全是单调数列
查看答案和解析>>
科目:高中数学 来源: 题型:
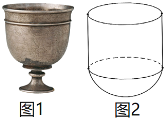
【题目】唐朝的狩猎景象浮雕银杯如图1所示.其浮雕临摹了国画、漆绘和墓室壁画,体现了古人的智慧与工艺.它的盛酒部分可以近似地看作是半球与圆柱的组合体(假设内壁表面光滑,忽略杯壁厚度),如图2所示.已知球的半径为R,酒杯内壁表面积为![]() ,设酒杯上部分(圆柱)的体积为
,设酒杯上部分(圆柱)的体积为![]() ,下部分(半球)的体积为
,下部分(半球)的体积为![]() ,则
,则![]() ( )
( )
A.2B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年新型冠状病毒肺炎(简称“新冠肺炎”)成为威胁全球的公共卫生问题,中医药在本次新冠肺炎的治疗中发挥了重要作用.研究人员对66例普通型新冠肺炎恢复期患者进行了中医临床特征分析,发现主要证型有气阴两虚证与肺脾气虚证,同时可能兼夹湿证.为研究这两种主要证型在兼夹湿证的难易上是否有差异,研究人员将湿证症状分级量化,将所有肺脾气虚证患者的量化分作成茎叶图.
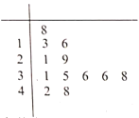
(1)若量化分不低于16分,即可诊断为兼夹湿证,请参考茎叶图,完成下面![]() 列联表.
列联表.
夹湿证 | 非夹湿证 | 合计 | |
气阴两虚 | 20 | ||
肺脾气虚 | |||
合计 | 66 |
(2)根据此资料,能否有99%的把握认为两种主要证型在兼夹湿证的难易上有差异?
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
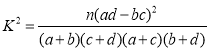
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ex+asinx,x∈(-π,+∞),下列说法正确的是( )
A.当a=1时,f(x)在(0,f(0))处的切线方程为2x-y+1=0
B.当a=1时,f(x)存在唯一极小值点x0且-1<f(x0)<0
C.对任意a>0,f(x)在(-π,+∞)上均存在零点
D.存在a<0,f(x)在(-π,+∞)上有且只有一个零点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com