
已知函数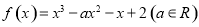 .
.
(1)当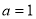 时,求函数
时,求函数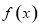 的极值;
的极值;
(2)若对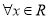 ,有
,有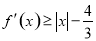 成立,求实数
成立,求实数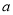 的取值范围.
的取值范围.
(1)极大值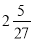 ,极小值
,极小值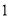 ;(2)
;(2)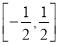 .
.
【解析】
试题分析:(1)将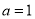 代入函数
代入函数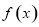 的解析式,利用导数结合表格求出函数
的解析式,利用导数结合表格求出函数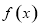 的极大值与极小值;(2)对
的极大值与极小值;(2)对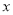 的符号进行分三类讨论①
的符号进行分三类讨论①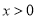 ;②
;②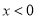 ;③
;③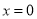 ,主要是取绝对值符号,结合基本不等式求出参数
,主要是取绝对值符号,结合基本不等式求出参数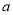 的取值范围,最后再相应地取
的取值范围,最后再相应地取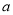 在三种情况下对应取值范围的交集.
在三种情况下对应取值范围的交集.
(1)当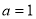 时,
时,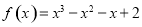 ,
,
 ,
,
令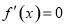 ,解得
,解得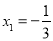 ,
, ,
,
当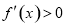 时,得
时,得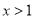 或
或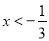 ;
;
当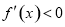 时,得
时,得 ,
,
当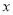 变化时,
变化时,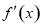 ,
,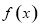 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
| 单调递增 | 极大 | 单调递减 | 极小 | 单调递增 |
 当
当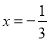 时,函数
时,函数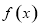 有极大值,
有极大值, ,
,
当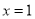 时函数
时函数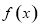 有极小值,
有极小值,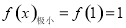 ;
;
(2)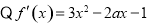 ,
, 对
对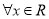 ,
,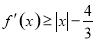 成立,
成立,
即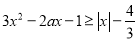 对
对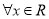 成立;
成立;
①当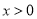 时,有
时,有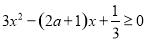 ,
,
即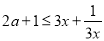 ,对
,对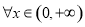 恒成立,
恒成立,
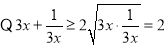 ,当且仅当
,当且仅当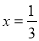 时等号成立,
时等号成立,
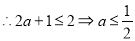 ;
;
②当 时,有
时,有 ,
,
即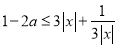 ,对
,对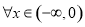 恒成立,
恒成立,
 ,当且仅当
,当且仅当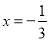 时等号成立,
时等号成立,
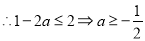 ,
,
③当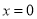 时,
时,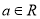
综上得实数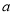 的取值范围为
的取值范围为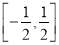 .
.
考点:1.函数的极值与导数;2.函数不等式恒成立;3.基本不等式;4.参变量分离法


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源:2013-2014学年广东省惠州市高三4月模拟考试文科数学试卷(解析版) 题型:选择题
用二分法求方程 的近似解,可以取的一个区间是( )
的近似解,可以取的一个区间是( )
A.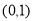 B.
B.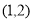 C.
C.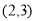 D.
D.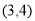
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省广州市毕业班综合测试二文科数学试卷(解析版) 题型:选择题
设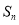 是等差数列
是等差数列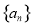 的前
的前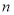 项和,公差
项和,公差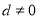 ,若
,若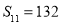 ,若
,若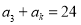 ,则正整数
,则正整数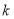 的值为( )
的值为( )
A.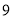 B.
B.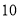 C.
C.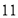 D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省东莞市高三第二次模拟考试文科数学试卷(解析版) 题型:填空题
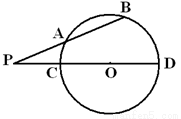
如图,圆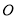 的割线
的割线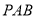 交圆
交圆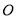 于
于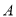 、
、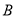 两点,割线
两点,割线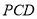 经过圆心
经过圆心 ,已知
,已知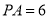 ,
,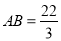 ,
,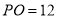 ,则圆
,则圆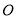 的半径是__ .
的半径是__ .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省东莞市高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
已知双曲线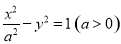 的右焦点与抛物线
的右焦点与抛物线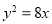 焦点重合,则此双曲线的渐近线方程是( )
焦点重合,则此双曲线的渐近线方程是( )
A.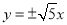 B.
B.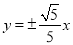
C.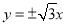 D.
D.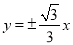
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省东莞市高三模拟(一)理科数学试卷(解析版) 题型:填空题
已知集合A={x|x2-2x-3>0 },B={x|ax2+bx+c≤0},若A∩B={x|3<x≤4},
A∪B=R,则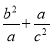 的最小值为____.
的最小值为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com