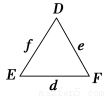
如图，在三棱锥S－ABC中，SA⊥SB，SB⊥SC，SA⊥SC，且SA、SB、
SC和底面ABC，所成的角分别为α1、α2、α3，三侧面SBC，SAC，SAB的面积分别为S1，S2，S3，类比三角形中的正弦定理，给出空间情形的一个猜想．
阶梯计算系列答案科目：高中数学 来源：2015届辽宁大连普通高中高二上学期期末考试文数学卷（解析版） 题型：解答题
已知函数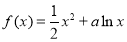
（
）.
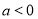(1)若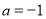
，求函数
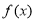的极值；
(2)若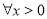
，不等式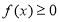
恒成立，求实数
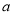的取值范围.
查看答案和解析>>
科目：高中数学 来源：2015届湘教版高二数学选修2-2基础达标6.3练习卷（解析版） 题型：选择题
用数学归纳法证明“n3＋(n＋1)3＋(n＋2)3，(n∈N＋)能被9整除”，要利
用归纳法假设证n＝k＋1时的情况，只需展开( )．
A．(k＋3)3 B．(k＋2)3
C．(k＋1)3 D．(k＋1)3＋(k＋2)3
查看答案和解析>>
科目：高中数学 来源：2015届湘教版高二数学选修2-2基础达标6.2练习卷（解析版） 题型：解答题
已知函数f(x)＝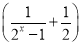
x3.
(1)判断f(x)的奇偶性；(2)求证：f(x)>0.
查看答案和解析>>
科目：高中数学 来源：2015届湘教版高二数学选修2-2基础达标6.1练习卷（解析版） 题型：填空题
定义在(0，＋∞)上的函数f(x)，满足(1)f(9)＝2；(2)对?a，b∈(0，＋
∞)，有f(ab)＝f(a)＋f(b)，则f
＝________.
查看答案和解析>>
科目：高中数学 来源：2015届湘教版高二数学选修2-2基础达标6.1练习卷（解析版） 题型：填空题
设函数f(x)＝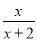
(x>0)，观察f1(x)＝f(x)＝
，
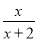f2(x)＝f[f1(x)]＝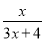
，
f3(x)＝f[f2(x)]＝
，
f4(x)＝f[f3(x)]＝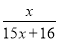
，…
根据以上事实，由归纳推理可得：当n∈N＋且n≥2时，fn(x)＝f[fn－1(x)]＝________.
查看答案和解析>>
科目：高中数学 来源：2015届湘教版高二数学选修2-2基础达标5章末练习卷（解析版） 题型：解答题
复数z＝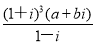
且|z|＝4，z对应的点在第一象限，若复数0，z，
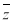对应的点是正三角形的三个顶点，求实数a、b的值．
查看答案和解析>>
科目：高中数学 来源：2015届湘教版高二数学选修2-2基础达标5.4练习卷（解析版） 题型：解答题
已知复数z1满足(z1－2)(1＋i)＝1－i，复数z2的虚
部为2，且z1z2为实数，求z2及|z2|.
查看答案和解析>>
科目：高中数学 来源：2015届湘教版高二数学选修2-2基础达标4章末练习卷（解析版） 题型：填空题
过点P(－1,2)且与曲线y＝3x2－4x＋2在点M(1,1)处的切线平行的直线
方程是________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
