练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

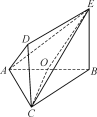
    【题目】已知空间四边形ABCD，，，，，且平面平面BCD，则该几何体的外接球的表面积为（　　）

    A.B.C.D.

    【答案】B

    【解析】

    由题意画出图形，找出外接球的球心，求解三角形得到半径，代入球的表面积公式求解．

    如图所示，取BC中点E，连接AE并延长至的外心G，在中，由，，

    可得BE＝CE＝3，则BC＝6，又，，满足，则是为以BD为斜边的直角三角形，

    则BD中点F为的外心，∵平面ABC⊥平面BCD，过F作平面BCD的垂线与过G作平面ABC的垂线相交于O，

    ∴O为空间四边形ABCD的外接球的球心．在中，由正弦定理得，得AG＝2．

    ∴，则OF＝，∴空间四边形ABCD的外接球的半径R＝OD＝．

    ∴空间四边形ABCD的外接球的表面积．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，AC⊥BC，O为AB中点，且DC⊥平面ABC，DC∥BE.已知AC＝BC＝DC＝BE＝2.

    （1）求直线AD与CE所成角；

    （2）求二面角O-CE-B的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】市场上有一种新型的强力洗衣粉，特点是去污速度快，已知每投放（且）个单位的洗衣粉液在一定量水的洗衣机中，它在水中释放的浓度（克/升）随着时间（分钟）变化的函数关系式近似为，其中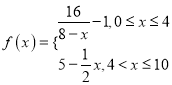，若多次投放，则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和，根据经验，当水中洗衣液的浓度不低于4（克/升）时，它才能起有效去污的作用.

    （1）若只投放一次4个单位的洗衣液，则有效去污时间可能达几分钟？

    （2）若先投放2个单位的洗衣液，6分钟后投放个单位的洗衣液，要使接下来的4分钟中能够持续有效去污，试求的最小值（精确到0.1，参考数据： 取）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】经过多年的努力，炎陵黄桃在国内乃至国际上逐渐打开了销路，成为炎陵部分农民脱贫致富的好产品.为了更好地销售，现从某村的黄桃树上随机摘下了100个黄桃进行测重，其质量分布在区间内（单位：克），统计质量的数据作出其频率分布直方图如图所示：

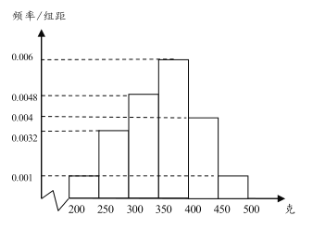
    （1）按分层抽样的方法从质量落在，的黄桃中随机抽取5个，再从这5个黄桃中随机抽2个，求这2个黄桃质量至少有一个不小于400克的概率；

    （2）以各组数据的中间数值代表这组数据的平均水平，以频率代表概率，已知该村的黄桃树上大约还有100000个黄桃待出售，某电商提出两种收购方案：

    A.所有黄桃均以20元/千克收购；

    B.低于350克的黄桃以5元/个收购，高于或等于350克的以9元/个收购.

    请你通过计算为该村选择收益最好的方案.

    （参考数据：）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一,为坚决打赢脱贫攻坚战，某帮扶单位为帮助定点扶贫村扶贫. 此帮扶单位为了了解某地区贫困户对其所提供的帮扶的满意度，随机调查了40个贫困户，得到贫困户的满意度评分如下：

    贫困户编号

    评分

    贫困户编号

    评分

    贫困户编号

    评分

    贫困户编号

    评分

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    78

    73

    81

    92

    95

    85

    79

    84

    63

    86

    11

    12

    13

    14

    15

    16

    17

    18

    19

    20

    88

    86

    95

    76

    97

    78

    88

    82

    76

    89

    21

    22

    23

    24

    25

    26

    27

    28

    29

    30

    79

    83

    72

    74

    91

    66

    80

    83

    74

    82

    31

    32

    33

    34

    35

    36

    37

    38

    39

    40

    93

    78

    75

    81

    84

    77

    81

    76

    85

    89

    用系统抽样法从40名贫困户中抽取容量为10的样本，且在第一分段里随机抽到的评分数据为92.

    （1）请你列出抽到的10个样本的评分数据；

    （2）计算所抽到的10个样本的均值和方差；

    （3）在（2）条件下，若贫困户的满意度评分在之间，则满意度等级为“级”.运用样本估计总体的思想，现从（1）中抽到的10个样本的满意度为“级”贫困户中随机地抽取2户，求所抽到2户的满意度均评分均“超过80”的概率.

    （参考数据：）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，，是的导函数.

    （1）若，求在处的切线方程；

    （2）若在可上单调递增，求的取值范围；

    （3）求证：当时在区间内存在唯一极大值点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为庆祝建国70周年，校园文化节举行有奖答题活动，现有A，B两种题型，从A类题型中抽取1道，从B类题型中抽取2道回答，答对3道题获新华书店面值为15元的图书代金券，答对2道题获面值为10元的图书代金券，答对1道题获面值为5元的图书代金券，没有答对获面值为1元的图书代金券（作为鼓励）.甲同学参加此活动答对A类题的概率为，答对B类题的概率为.

    （Ⅰ）求甲答对1道题的概率；

    （Ⅱ）设甲参加一次活动所获图书代金券的面值为随机变量X，求X的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】

    如图，长方体ABCD–A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1.

    （1）证明：BE⊥平面EB1C1；

    （2）若AE=A1E，求二面角B–EC–C1的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】的内角、、的对边分别为，，，点为的中点，已知，，.

    （1）求角的大小和的长；

    （2）设的角平分线交于，求的面积.

    查看答案和解析>>

    同步练习册答案