
 上存在单调递增区间,试求实数a的取值范围;
上存在单调递增区间,试求实数a的取值范围; ,
,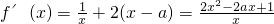
 上存在子区间使得不等式g(x)>0成立.…(5分)
上存在子区间使得不等式g(x)>0成立.…(5分)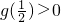 即可.…(6分)
即可.…(6分)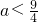 ,
,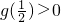 ,即
,即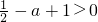 ,得
,得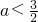 ,
,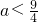 ,
, .…(8分)
.…(8分)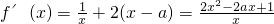 ,…(4分)
,…(4分) ,2]上存在子区间使不等式2x2-2ax+1>0成立.
,2]上存在子区间使不等式2x2-2ax+1>0成立.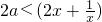 .…(5分)
.…(5分) ,所以2a小于函数g(x)在区间[
,所以2a小于函数g(x)在区间[ ,2]的最大值.
,2]的最大值.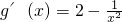 ,
,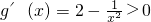 ,解得
,解得 ;
;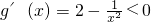 ,解得
,解得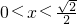 .
.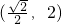 上递增,在区间
上递增,在区间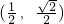 上递减.
上递减. ,或x=2处取得最大值.
,或x=2处取得最大值.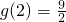 ,
,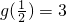 ,所以
,所以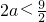 ,
,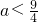
 .…(8分)
.…(8分)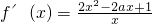 ,令h(x)=2x2-2ax+1
,令h(x)=2x2-2ax+1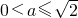 时,
时, 时,
时, 时,
时,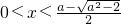 或
或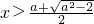 时,
时, 时,
时,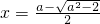 是函数f(x)的极大值点;
是函数f(x)的极大值点;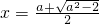 是函数f(x)的极小值点.…(12分)
是函数f(x)的极小值点.…(12分)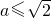 时,函数f(x)没有极值点;
时,函数f(x)没有极值点; 时,
时,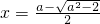 是函数f(x)的极大值点;
是函数f(x)的极大值点;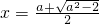 是函数f(x)的极小值点.…(13分)
是函数f(x)的极小值点.…(13分) ,所以f(x)在[1,e]上是增函数,由此能求出f(x)在[1,e]上的最小值.
,所以f(x)在[1,e]上是增函数,由此能求出f(x)在[1,e]上的最小值.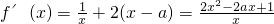 ,设g(x)=2x2-2ax+1,则在区间
,设g(x)=2x2-2ax+1,则在区间 上存在子区间使得不等式g(x)>0成立.由抛物线g(x)=2x2-2ax+1开口向上,所以只要g(2)>0,或
上存在子区间使得不等式g(x)>0成立.由抛物线g(x)=2x2-2ax+1开口向上,所以只要g(2)>0,或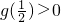 即可.由此能求出实数a的取值范围.
即可.由此能求出实数a的取值范围.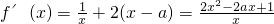 ,则在区间[
,则在区间[ ,2]上存在子区间使不等式2x2-2ax+1>0成立.因为x>0,所以
,2]上存在子区间使不等式2x2-2ax+1>0成立.因为x>0,所以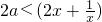 .设g(x)=2x+
.设g(x)=2x+ ,所以2a小于函数g(x)在区间[
,所以2a小于函数g(x)在区间[ ,2]的最大值.由此能求出实数a的取值范围.
,2]的最大值.由此能求出实数a的取值范围.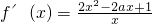 ,令h(x)=2x2-2ax+1.由a≤0,a>0及判别式△的符号分别进行讨论,求解函数f(x)的极值点.
,令h(x)=2x2-2ax+1.由a≤0,a>0及判别式△的符号分别进行讨论,求解函数f(x)的极值点.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| e | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2x |
| x+2 |
| 9 |
| 10 |
| 1 |
| e2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 | x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 2 |
| x |
| 3 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com