
����Ŀ��Ϊ����ǿ������ʶ��ij���Ŵ������������ȡ��60�ˣ���Ů���������ȡ��50�˲μӻ���֪ʶ���ԣ�ͳ���������±���ʾ��
���� | ������ | �ܼ� | |
���� | 40 | 20 | 60 |
�� | 20 | 30 | 50 |
�ܼ� | 60 | 50 | 110 |
��1�����ж��Ƿ���99%�İ�����Ϊ����֪ʶ�Ƿ��������Ա��йأ�
��2��Ϊ�μ��оٰ�Ļ���֪ʶ������ѧУ�ٰ�Ԥѡ�������ڻ������������ͬѧ��ѡ3�˲μ�Ԥѡ������֪�ڻ��������������ͬѧͨ��Ԥѡ���ĸ���Ϊ![]() �����������
�����������![]() ��ʾ��3����ͨ��Ԥѡ������������
��ʾ��3����ͨ��Ԥѡ������������![]() �ķֲ�������ѧ������
�ķֲ�������ѧ������
��:![]() ��
��![]()
| 0��500 | 0��400 | 0��100 | 0��010 | 0��001 |
| 0��455 | 0��708 | 2��706 | 6��635 | 10��828 |

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijũ�����Զ�����ҹ�²��С��ij�����ڴ���Ʒ�ַ�ѿ����֮��Ĺ�ϵ���з����о������Ƿֱ��¼��12��1����12��5�յ�ÿ����ҹ�²���ʵ����ÿ��ÿ100�������еķ�ѿ�����õ��������ϣ�
�� �� | 12��1�� | 12��2�� | 12��3�� | 12��4�� | 12��5�� |
�²� | 10 | 11 | 13 | 12 | 8 |
��ѿ�� | 23 | 25 | 30 | 26 | 16 |
��ũ����ȷ�����о�������:�ȴ�������������ѡȡ2�飬��ʣ�µ�3�����������Իع鷽�̣��ٶԱ�ѡȡ��2�����ݽ��м��飮
��1����ѡȡ��2������ǡ���Dz�����2�����ݵĸ��ʣ�
��2����ѡȡ����12��1����12��5�յ��������ݣ������12��2����12��4�յ����ݣ����y����x�����Իع鷽��![]() ��
��
��3���������Իع鷽�̵õ��Ĺ�����������ѡ���ļ������ݵ�����������2�ţ�����Ϊ�õ������Իع鷽���ǿɿ��ģ����ʣ�2�������õ����Իع鷽���Ƿ�ɿ���
��ע�� 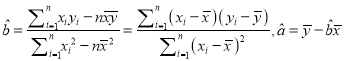 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�����Ƴ�һ�����������ֻ���Ϊ�˸��õضԲ�Ʒ������������Ԥ��������ÿ��ֻ��Ƿ��������йأ��������ȡ��50��������й�����Ը���ʾ����飬���÷ֵ���60�֣�˵��������Ը�������÷ֲ�����60�֣�˵��������Ըǿ���������þ�Ҷͼ��ʾ��ͼ��ʾ.
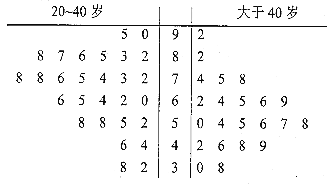
��1�����ݾ�Ҷͼ�е��������![]() �����������ж��Ƿ���95%�İ�����Ϊ�����Ƿ���ÿ��ֻ��������йأ�
�����������ж��Ƿ���95%�İ�����Ϊ�����Ƿ���ÿ��ֻ��������йأ�
������Ըǿ | ������Ը�� | �ϼ� | |
20~40�� | |||
����40�� | |||
�ϼ� |
��2���ӹ�����Ը���������а�������зֲ����������ȡ5�ˣ�����5���������ȡ2�˽��вɷã��dz鵽��2�����������40�����������Ϊ![]() ����
����![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.
����![]() .
.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() ����.
����.
��1�����ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
��2����![]() ����������ֵ��
����������ֵ��![]() ����֤������ʵ��
����֤������ʵ��![]() ȡʲôֵ����
ȡʲôֵ����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������˵����
�������ָ��R2���̻��ع�Ч����R2ԽС��˵��ģ�͵����Ч��Խ�ã�
������P����x0��R��x02��x0��1��0���ķ��ǩVP����x��R��x2��x��1��0����
�����������X������̬�ֲ�N��0��1������P��x��1��=p��P����1��X��0��=![]() ��p
��p
�ܻع�ֱ��һ��������������ģ�![]() ����
����
������ȷ��˵���У� ��
A. �٢ڢ� B. �٢ڢ� C. �ڢۢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=![]()
![]() ��t+1��lnx��������t��R��
��t+1��lnx��������t��R��
��1����t=1����֤����x��1ʱ��f��x����0������
��2����t��![]() ���жϺ���g��x��=x[f��x��+t+1]�����ĸ�����
���жϺ���g��x��=x[f��x��+t+1]�����ĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f(x)�Ƕ��κ�����������f(0)��1��f(x��1)��f(x)��2x����f(x).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() Ϊ������,
������, ![]() ��
��![]() �ϵĶ��㣬������
�ϵĶ��㣬������![]() Ϊ����ԭ��)����ԭ��
Ϊ����ԭ��)����ԭ��![]() Ϊ���㣬
Ϊ���㣬 ![]() ���������Ϊ���Ὠ������ϵ����
���������Ϊ���Ὠ������ϵ����![]() �ļ�����Ϊ
�ļ�����Ϊ![]() .
.
��1�����߶�![]() ���е�
���е�![]() �Ĺ켣
�Ĺ켣![]() ����ͨ���̣�
����ͨ���̣�
��2��������Բ![]() �ļ����귽��֤��
�ļ����귽��֤��![]() Ϊ��ֵ��������������ֵ.
Ϊ��ֵ��������������ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com