
【题目】已知抛物线![]() 的准线与双曲线
的准线与双曲线![]() 相交于
相交于![]() 、
、![]() 两点,双曲线的一条渐近线方程是
两点,双曲线的一条渐近线方程是![]() ,点
,点![]() 是抛物线的焦点,且
是抛物线的焦点,且![]() 是等边三角形,则该双曲线的标准方程是( )
是等边三角形,则该双曲线的标准方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】在测试中,客观题难度的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 题的难度,
题的难度, ![]() 为答对该题的人数,
为答对该题的人数, ![]() 为参加测试的总人数.现对某校高三年级240名学生进行一次测试,共5道客观题,测试前根据对学生的了解,预估了每道题的难度,如表所示:
为参加测试的总人数.现对某校高三年级240名学生进行一次测试,共5道客观题,测试前根据对学生的了解,预估了每道题的难度,如表所示:
题号 | 1 | 2 | 3 | 4 | 5 |
考前预估难度 | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
测试后,从中随机抽取了20名学生的答题数据进行统计,结果如表:

(Ⅰ)根据题中数据,估计中240名学生中第5题的实测答对人数;
(Ⅱ)从抽样的20名学生中随机抽取2名学生,记这2名学生中第5题答对的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)试题的预估难度和实测难度之间会有偏差.设![]() 为第
为第![]() 题的实测难度,请用
题的实测难度,请用![]() 和
和![]() 设计一个统计量,并制定一个标准来判断本次测试对难度的预估是否合理.
设计一个统计量,并制定一个标准来判断本次测试对难度的预估是否合理.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,G是线段AD延长线一点,![]() ,
,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,F是线段PG的中点;
,F是线段PG的中点;

![]() 求证:
求证:![]() 平面PAC;
平面PAC;
![]() 若
若![]() 时,求平面PCF与平面PAG所成二面角的余弦值.
时,求平面PCF与平面PAG所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】1642年,帕斯卡发明了一种可以进行十进制加减法的机械计算机![]() 年,莱布尼茨改进了帕斯卡的计算机,但莱布尼兹认为十进制的运算在计算机上实现起来过于复杂,随即提出了“二进制”数的概念
年,莱布尼茨改进了帕斯卡的计算机,但莱布尼兹认为十进制的运算在计算机上实现起来过于复杂,随即提出了“二进制”数的概念![]() 之后,人们对进位制的效率问题进行了深入的研究
之后,人们对进位制的效率问题进行了深入的研究![]() 研究方法如下:对于正整数
研究方法如下:对于正整数![]() ,
,![]() ,我们准备
,我们准备![]() 张不同的卡片,其中写有数字0,1,…,
张不同的卡片,其中写有数字0,1,…,![]() 的卡片各有
的卡片各有![]() 张
张![]() 如果用这些卡片表示
如果用这些卡片表示![]() 位
位![]() 进制数,通过不同的卡片组合,这些卡片可以表示
进制数,通过不同的卡片组合,这些卡片可以表示![]() 个不同的整数
个不同的整数![]() 例如
例如![]() ,
,![]() 时,我们可以表示出
时,我们可以表示出![]() 共
共![]() 个不同的整数
个不同的整数![]() 假设卡片的总数
假设卡片的总数![]() 为一个定值,那么
为一个定值,那么![]() 进制的效率最高则意味着
进制的效率最高则意味着![]() 张卡片所表示的不同整数的个数
张卡片所表示的不同整数的个数![]() 最大
最大![]() 根据上述研究方法,几进制的效率最高?
根据上述研究方法,几进制的效率最高?![]()
![]()
A. 二进制 B. 三进制 C. 十进制 D. 十六进制
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】田忌赛马是![]() 史记
史记![]() 中记载的一个故事,说的是齐国将军田忌经常与齐国众公子赛马,孙膑发也们的马脚力都差不多,都分为上、中、下三等
中记载的一个故事,说的是齐国将军田忌经常与齐国众公子赛马,孙膑发也们的马脚力都差不多,都分为上、中、下三等![]() 于是孙膑给田忌将军制定了一个必胜策略:比赛即将开始时,他让田忌用下等马对战公子们的上等马,用上等马对战公子们的中等马,用中等马对战公子们的下等马,从而使田忌赢得公子们许多赌注
于是孙膑给田忌将军制定了一个必胜策略:比赛即将开始时,他让田忌用下等马对战公子们的上等马,用上等马对战公子们的中等马,用中等马对战公子们的下等马,从而使田忌赢得公子们许多赌注![]() 假设田忌的各等级马与某公子的各等级马进行一场比赛获胜的概率如表所示:
假设田忌的各等级马与某公子的各等级马进行一场比赛获胜的概率如表所示:
田忌的马 | 上等马 | 中等马 | 下等马 |
上等马 |
|
| 1 |
中等马 |
|
|
|
下等马 | 0 |
|
|
比赛规则规定:一次比由三场赛马组成,每场由公子和田忌各出一匹马出骞,结果只有胜和负两种,并且毎一方三场赛马的马的等级各不相同,三场比赛中至少获胜两场的一方为最终胜利者.
![]() 如果按孙膑的策略比赛一次,求田忌获胜的概率;
如果按孙膑的策略比赛一次,求田忌获胜的概率;
![]() 如果比赛约定,只能同等级马对战,每次比赛赌注1000金,即胜利者赢得对方1000金,每月比赛一次,求田忌一年赛马获利的数学期望.
如果比赛约定,只能同等级马对战,每次比赛赌注1000金,即胜利者赢得对方1000金,每月比赛一次,求田忌一年赛马获利的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
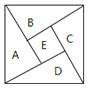
【题目】如图为我国数学家赵爽![]() 约3世纪初
约3世纪初![]() 在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则
在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则![]() 区域涂色不相同的概率为
区域涂色不相同的概率为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com