
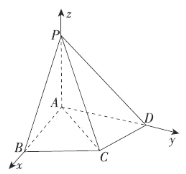
【题目】如图,在四棱锥![]() 中,
中,![]() 为正三角形,
为正三角形,![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() .
.

(Ⅰ)点![]() 在棱
在棱![]() 上,试确定点
上,试确定点![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)当![]() 为
为![]() 中点时
中点时![]() .(Ⅱ)二面角
.(Ⅱ)二面角![]() 的余弦值为
的余弦值为![]() .
.
【解析】
试题分析:(Ⅰ)根据题意,以![]() 为坐标原点,射线
为坐标原点,射线![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴的正方向建立空间直角坐标系,设
轴的正方向建立空间直角坐标系,设![]() ,若
,若![]() ,则
,则![]() ,即
,即![]() ,在空间直角坐标系中求出相应向量坐标,可求出
,在空间直角坐标系中求出相应向量坐标,可求出![]() ,由此确定点
,由此确定点![]() 的位置(Ⅱ)在空间直角坐标系中求出平面
的位置(Ⅱ)在空间直角坐标系中求出平面![]() 的一个法向量
的一个法向量![]() ,再求出平面
,再求出平面![]() 的一个法向量
的一个法向量![]() ,利用夹角公式即可求得二面角
,利用夹角公式即可求得二面角![]() 的余弦值.
的余弦值.
试题解析:
(Ⅰ)∵![]() ∴
∴![]() ;又∵
;又∵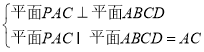 ,∴
,∴![]() ,可得
,可得![]() ,
,![]() ,以
,以![]() 为坐标原点,射线
为坐标原点,射线![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴的正方向建立空间直角坐标系,设
轴的正方向建立空间直角坐标系,设![]() ,则
,则![]() ,
,![]() ,
,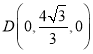 ,
,![]() .
.
(Ⅰ)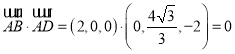 ,故
,故![]() ;
;
设![]() ,若
,若![]() ,则
,则![]() ,即
,即![]() ,
,
即![]() ,即
,即![]() ,即当
,即当![]() 为
为![]() 中点时,
中点时,![]() ,
,
则![]() .所以当
.所以当![]() 为
为![]() 中点时
中点时![]() .
.
(Ⅱ)设平面![]() 的一个法向量
的一个法向量![]() ,
,
![]() ,
,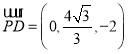 ,则
,则![]() 且
且![]() ,
,
即![]() 且
且![]() ,
,
令![]() ,则
,则![]() ,
,![]() ,则
,则![]() ,
,
再取平面![]() 的一个法向量
的一个法向量![]() .
.
则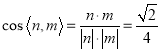 ,
,
故二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】设甲、乙、丙三个乒乓球协会的运动员人数分别为27,9,18,先采用分层抽样的方法从这三个协会中抽取6名运动员参加比赛.
(Ⅰ)求应从这三个协会中分别抽取的运动员人数;
(Ⅱ)将抽取的6名运动员进行编号,编号分别为![]() ,从这6名运动员中随机抽取2名参加双打比赛.
,从这6名运动员中随机抽取2名参加双打比赛.
(ⅰ)用所给编号列出所有可能的结果;
(ⅱ)设![]() 为事件“编号为
为事件“编号为![]() 的两名运动员至少有一人被抽到”,求事件
的两名运动员至少有一人被抽到”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生身高情况,某校以![]() 的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为
的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为![]() ,测得男生身高情况的频率分布直方图(如图所示):
,测得男生身高情况的频率分布直方图(如图所示):
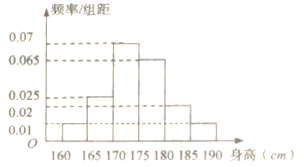
(1)计算所抽取的男生人数,并估计男生身高的中位数(保留两位小数);
(2)从样本中身高在![]() 之间的男生中任选2人,求至少有1人身高在
之间的男生中任选2人,求至少有1人身高在![]() 之间的概率.
之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品,已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为:![]() ,且每处理一顿二氧化碳得到可利用的化工产品价值为100元.
,且每处理一顿二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家每月至少需要补贴多少元才能使该单位不亏损?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数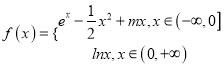 ,
, ![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)若函数![]() 的图象在
的图象在![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(2)若![]() 时,函数
时,函数![]() 在
在![]() 内是增函数,求
内是增函数,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,设函数
时,设函数![]() 的图象
的图象![]() 与函数
与函数![]() 的图象
的图象![]() 交于点
交于点![]() 、
、![]() ,过线段
,过线段![]() 的中点
的中点![]() 作
作![]() 轴的垂线分别交
轴的垂线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,问是否存在点
,问是否存在点![]() ,使
,使![]() 在
在![]() 处的切线与
处的切线与![]() 在
在![]() 处的切线平行?若存在,求出
处的切线平行?若存在,求出![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com