
【题目】下列结论中正确的是__________.
①将一组数据中的每个数据都加上或减去同一个常数后,方差不变;
②在吸烟与患肺病这两个分类变量的独立性检验中,“有99%的把握认为吸烟与患肺病有关”的含义是“若某人吸烟,则他有99%的可能患肺病;”
③已知“![]() ”为真命题,则“
”为真命题,则“![]() ”、“
”、“![]() ”、“
”、“![]() ”中至少有一个真命题;
”中至少有一个真命题;
④以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,其变换后得到线性回归方程
,其变换后得到线性回归方程![]() 则
则![]() .
.
【答案】①③④.
【解析】分析:①根据方差的性质进行判断;
②有99%的把握认为吸烟与患肺病有关系,表示有1%的可能性使推断出现错误,不表示有99%的可能患有肺病判断;
③由“![]() ”为真命题,可得p,q中至少有一个真命题,即可判定;
”为真命题,可得p,q中至少有一个真命题,即可判定;
④根据对数的运算性质即可得出结论.
详解:对于①,将一组数据中的每个数据都加上或减去同一个常数后,根据方差的性质得方差不变,故①正确;
对于②,在吸烟与患肺病这两个分类变量的独立性检验中,“有99%的把握认为吸烟与患肺病有关”的含义是“有1%的可能性使推断出现错误,不表示有99%的可能患有肺病”,故②错误;
对于③,由“![]() ”为真命题,可得p,q中至少有一个真命题,则“
”为真命题,可得p,q中至少有一个真命题,则“![]() ”、“
”、“![]() ”、“
”、“![]() ”中至少有一个真命题,故③正确;
”中至少有一个真命题,故③正确;
对于④,![]() 两边取对数,可得
两边取对数,可得![]() ,可得
,可得![]() ,其变换后得到线性回归方程
,其变换后得到线性回归方程![]() ,则
,则![]() ,故④正确.
,故④正确.
故答案为:①③④.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() :
:![]() .设圆
.设圆![]() 的半径为1,圆心在
的半径为1,圆心在![]() 上.
上.

(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆心![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读如下程序框图,如果输出i=5,那么在空白矩形框中应填入的语句为( ) 
A.S=2*i﹣2
B.S=2*i﹣1
C.S=2*I
D.S=2*i+4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问110名不同的大学生是否爱好某项运动,得到如下的列联表:
经计算![]() 的观测值
的观测值![]() . 参照附表,得到的正确结论是
. 参照附表,得到的正确结论是
附表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
A. 有99%以上的把握认为“爱好该项运动与性别有关”
B. 有99%以上的把握认为“爱好该项运动与性别无关”
C. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的三角形ABC中,一机器人从三角形ABC上的每一个顶点移动到另一个顶点,(规定:每次只能从一个顶点移动到另一个顶点),而且按逆时针方向移动的概率为顺时针方向移动的概率的3倍,假设现在机器人的初始位置为顶点A处,则通过三次移动后返回到A处的概率为________________________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,a为常数且a>0.
,a为常数且a>0.
(1)f(x)的图象关于直线x= ![]() 对称;
对称;
(2)若x0满足f(f(x0))=x0 , 但f(x0)≠x0 , 则x0称为函数f(x)的二阶周期点,如果f(x)有两个二阶周期点x1 , x2 , 试确定a的取值范围;
(3)对于(2)中的x1 , x2 , 和a,设x3为函数f(f(x))的最大值点,A(x1 , f(f(x1))),B(x2 , f(f(x2))),C(x3 , 0),记△ABC的面积为S(a),讨论S(a)的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
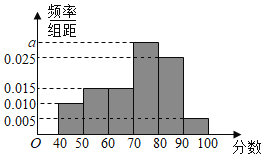
【题目】某校从高二年级学生中随机抽取60名学生,将期中考试的政治成绩(均为整数)分成六段:![]() 后得到如下频率分布直方图.
后得到如下频率分布直方图.
(1)根据频率分布直方图,分别求![]() ,众数,中位数。
,众数,中位数。
(2)估计该校高二年级学生期中考试政治成绩的平均分。
(3)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则在![]() 分数段抽取的人数是多少?
分数段抽取的人数是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二文科分四个班,各班人数恰好成等差数列,高二数学调研测试后,对四个文科班的学生试卷按每班人数进行分层抽样,对测试成绩进行统计,人数最少的班抽取了![]() 人,抽取的所有学生成绩分为
人,抽取的所有学生成绩分为![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图,其中第六组分数段的人数为
,得到如图所示的频率分布直方图,其中第六组分数段的人数为![]() 人.
人.
(![]() )求
)求![]() 的值,并求出各班抽取的学生数各为多少人?
的值,并求出各班抽取的学生数各为多少人?
(![]() )在抽取的学生中,任取一名学生,求分数不小于
)在抽取的学生中,任取一名学生,求分数不小于![]() 分的概率(视频率为概率).
分的概率(视频率为概率).
(![]() )估计高二文科四个班数学成绩的平均分
)估计高二文科四个班数学成绩的平均分

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com