
【题目】已知四棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 中点.
中点.
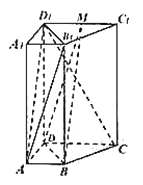
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:
【题目】如下图,汉诺塔问题是指有3根杆子A,B,C.B杆上有若干碟子,把所有碟子从B杆移到A杆上,每次只能移动一个碟子,大的碟子不能叠在小的碟子上面.把B杆上的4个碟子全部移到A杆上,最少需要移动( )次. ( )



A.12 B.15 C.17 D.19
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的个数是( )
①一组数据的标准差越大,则说明这组数据越集中;
②曲线![]() 与曲线
与曲线![]() 的焦距相等;
的焦距相等;
③在频率分布直方图中,估计的中位数左边和右边的直方图的面积相等;
④已知椭圆![]() ,过点
,过点![]() 作直线,当直线斜率为
作直线,当直线斜率为![]() 时,M刚好是直线被椭圆截得的弦AB的中点.
时,M刚好是直线被椭圆截得的弦AB的中点.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() 的焦距为
的焦距为![]() ,直线
,直线![]() 截圆
截圆![]() 与椭圆
与椭圆![]() 所得的弦长之比为
所得的弦长之比为![]() ,圆
,圆![]() 、椭圆
、椭圆![]() 与
与![]() 轴正半轴的交点分别为
轴正半轴的交点分别为![]() ,
,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() (
(![]() 且
且![]() )为椭圆
)为椭圆![]() 上一点,点
上一点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() ,
,![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,其中
,其中![]() ,则下列判断正确的是__________.(写出所有正确结论的序号)
,则下列判断正确的是__________.(写出所有正确结论的序号)
①![]() 关于点
关于点![]() 成中心对称;
成中心对称;
②![]() 在
在![]() 上单调递增;
上单调递增;
③存在![]() ,使
,使![]() ;
;
④若![]() 有零点,则
有零点,则![]() ;
;
⑤![]() 的解集可能为
的解集可能为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com