
【题目】设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为( )
A.y2=4x或y2=8x
B.y2=2x或y2=8x
C.y2=4x或y2=16x
D.y2=2x或y2=16x
【答案】C
【解析】解:∵抛物线C方程为y2=2px(p>0),
∴焦点F坐标为( ![]() ,0),可得|OF|=
,0),可得|OF|= ![]() ,
,
∵以MF为直径的圆过点(0,2),
∴设A(0,2),可得AF⊥AM,
Rt△AOF中,|AF|= ![]() =
= ![]() ,
,
∴sin∠OAF= ![]() =
= ![]() ,
,
∵根据抛物线的定义,得直线AO切以MF为直径的圆于A点,
∴∠OAF=∠AMF,可得Rt△AMF中,sin∠AMF= ![]() =
= ![]() ,
,
∵|MF|=5,|AF|= ![]()
∴ ![]() =
= ![]() ,整理得4+
,整理得4+ ![]() =
= ![]() ,解之可得p=2或p=8
,解之可得p=2或p=8
因此,抛物线C的方程为y2=4x或y2=16x.
故选:C.
方法二:
∵抛物线C方程为y2=2px(p>0),∴焦点F( ![]() ,0),
,0),
设M(x,y),由抛物线性质|MF|=x+ ![]() =5,可得x=5﹣
=5,可得x=5﹣ ![]() ,
,
因为圆心是MF的中点,所以根据中点坐标公式可得,圆心横坐标为 ![]() =
= ![]() ,
,
由已知圆半径也为 ![]() ,据此可知该圆与y轴相切于点(0,2),故圆心纵坐标为2,则M点纵坐标为4,
,据此可知该圆与y轴相切于点(0,2),故圆心纵坐标为2,则M点纵坐标为4,
即M(5﹣ ![]() ,4),代入抛物线方程得p2﹣10p+16=0,所以p=2或p=8.
,4),代入抛物线方程得p2﹣10p+16=0,所以p=2或p=8.
所以抛物线C的方程为y2=4x或y2=16x.
故答案C.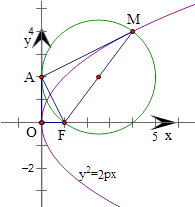
根据抛物线方程算出|OF|= ![]() ,设以MF为直径的圆过点A(0,2),在Rt△AOF中利用勾股定理算出|AF|=
,设以MF为直径的圆过点A(0,2),在Rt△AOF中利用勾股定理算出|AF|= ![]() .再由直线AO与以MF为直径的圆相切得到∠OAF=∠AMF,Rt△AMF中利用∠AMF的正弦建立关系式,从而得到关于p的方程,解之得到实数p的值,进而得到抛物线C的方程.
.再由直线AO与以MF为直径的圆相切得到∠OAF=∠AMF,Rt△AMF中利用∠AMF的正弦建立关系式,从而得到关于p的方程,解之得到实数p的值,进而得到抛物线C的方程.


科目:高中数学 来源: 题型:
【题目】随着我国经济模式的改变,电商已成为当今城乡种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出![]() 吨该商品可获利润
吨该商品可获利润![]() 万元,未售出的商品,每吨亏损
万元,未售出的商品,每吨亏损![]() 万元根据往年的销售资料,得到该商品一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了
万元根据往年的销售资料,得到该商品一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了![]() 吨该商品,现以
吨该商品,现以![]() 单位:吨,
单位:吨,![]() )表示下一个销售季度的市场需求量,
)表示下一个销售季度的市场需求量,![]() (单位:万 元)表示该电商下“个销售季度内经销该商品获得的利润.
(单位:万 元)表示该电商下“个销售季度内经销该商品获得的利润.

(1)视![]() 分布在各区间内的频率为相应的概率,求
分布在各区间内的频率为相应的概率,求![]() ;
;
(2)将![]() 表示为
表示为![]() 的函数,求出该函数表达式;
的函数,求出该函数表达式;
(3)在频率分布直方图的市场需求量分组中,若以市场需求量落入该区间的频率作为市场需求量的概率,求该季度利润不超过![]() 万元的概率.
万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】保险公司统计的资料表明:居民住宅距最近消防站的距离![]() (单位:千米)和火灾所造成的损失数额
(单位:千米)和火灾所造成的损失数额![]() (单位:千元)有如下的统计资料:
(单位:千元)有如下的统计资料:

(1)请用相关系数![]() (精确到0.01)说明
(精确到0.01)说明![]() 与
与![]() 之间具有线性相关关系;
之间具有线性相关关系;
(2)求![]() 关于
关于![]() 的线性回归方程(精确到0.01);
的线性回归方程(精确到0.01);
(3)若发生火灾的某居民区距最近的消防站10.0千米,请评估一下火灾损失(精确到0.01).
参考数据:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]()
参考公式:
回归直线方程为![]() ,其中
,其中 ,
,![]() ,
,![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一元二次函数的最大值为![]() ,其图象的对称轴为
,其图象的对称轴为![]() ,且与
,且与![]() 轴两个交点的横坐标的平方和为
轴两个交点的横坐标的平方和为![]() .
.
(1)求该一元二次函数;
(2)要将该函数图象的顶点平移到原点,请说出平移的方式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线C的方程为 ![]() ,点
,点 ![]() ,以极点为原点,极轴为x轴的正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
,以极点为原点,极轴为x轴的正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
(1)求曲线C的直角坐标方程及点R的直角坐标;
(2)设P为曲线C上一动点,以PR为对角线的矩形PQRS的一边垂直于极轴,求矩形PQRS周长的最小值及此时点P的直角坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com