
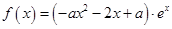 ,
,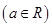
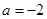 时,求函数
时,求函数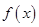 的极值;
的极值;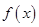 在[-1,1]上单调递减,求实数
在[-1,1]上单调递减,求实数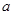 的取值范围.
的取值范围. 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源:不详 题型:解答题
 (0<
(0< <1
<1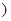 ,则出厂价相应提高的比例为0.7
,则出厂价相应提高的比例为0.7 ,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量. ,为使本年度的年利润比上年度有所增加,则投入成本增加的比例
,为使本年度的年利润比上年度有所增加,则投入成本增加的比例 应在什么范围内?
应在什么范围内? 的函数为
的函数为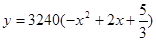 ,则当
,则当 为何值时,本年度的年利润最大?最大利润为多少?
为何值时,本年度的年利润最大?最大利润为多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
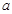 和
和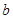 组成数对(
组成数对(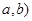 ,并构成函数
,并构成函数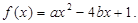
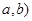 ,并计算
,并计算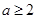 ,且
,且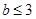 的概率;
的概率;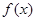 在区间[
在区间[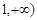 上是增函数的概率.
上是增函数的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com