Question

设椭圆C₂：

x2

a2

+

y2

b2

=1（a＞b＞0），抛物线C₂：x²+by=b²．
（1）若C₂经过C₁的两个焦点，求C₁的离心率；
（2）设A（0，b），Q(3

3

，

5

4

)，又M、N为C₁与C₂不在y轴上的两个交点，若△AMN的垂心为B(0，

3

4

b)，且△QMN的重心在C₂上，求椭圆C和抛物线C₂的方程．

Answer 1

分析：（1）由已知椭圆焦点（c，0）在抛物线上，可得：c²=b²，由a²=b²+c²，求得C₁的离心率；
（2）由题设可知M、N关于y轴对称，设M（-x₁，y₁），N（x₁，y₁）（x₁＞0），由△AMN的垂心为B，根据三角形的垂心是三条高线的交点，可知

BM

•

AN

=0，再根据三角形的重心坐标公式求得△QMN的重心，代入抛物线C₂：x²+by=b²，即可求得椭圆C和抛物线C₂的方程．

解答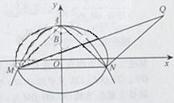：解：
（1）由已知椭圆焦点（c，0）在抛物线上，可得：c²=b²，
由a2=b2+c2=2c2，有

c2

a2

=

1

2

?e=

2

2

．
（2）由题设可知M、N关于y轴对称，设M（-x₁，y₁），N（x₁，y₁）（x₁＞0），由△AMN的垂心为B，有

BM

•

AN

=0?-

x

2 1

+(y1-

3

4

b)(y1-b)=0．
由点N（x₁，y₁）在抛物线上，x₁²+by₁=b²，解得：y1=-

b

4

或y1=b(舍去)
故x1=

5

2

b，M(-

5

2

b，-

b

4

)，N(

5

2

b，-

b

4

)，
得△QMN重心坐标(

3

，

b

4

)．
由重心在抛物线上得：3+

b2

4

=b2，所以b=2，M(-

5

，-

1

2

)，N(

5

，-

1

2

)，
又因为M、N在椭圆上得：a2=

16

3

，
椭圆方程为

x2

16 3

+

y2

4

=1，抛物线方程为x²+2y=4．

点评：此题是个中档题．考查椭圆和抛物线的定义、基本量，通过交点三角形来确认方程．考查抛物线的定义和简单的几何性质，特别是问题（2）的设问形式，增加了题目的难度，同时考查了三角的垂心和重心有关性质和公式，综合性强．